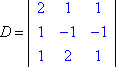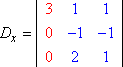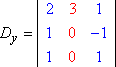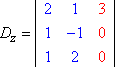Regla de Cramer

Dado un sistema de ecuaciones lineales, la regla de Cramer es una forma práctica de resolver sólo una de las variables sin tener que resolver todo el sistema de ecuaciones. No suelen enseñar la Regla de Cramer de esta manera, pero se supone que este es el objetivo de la Regla: en lugar de resolver todo el sistema de ecuaciones, puedes usar la de Cramer para resolver una sola variable.

Usemos el siguiente sistema de ecuaciones:

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

Tenemos el lado izquierdo del sistema con las variables (la «matriz de coeficientes») y el lado derecho con los valores de la respuesta. Sea D el determinante de la matriz de coeficientes del sistema anterior, y sea Dx el determinante que se forma sustituyendo los valores de la columna x por los de la columna respuesta:

sistema de ecuaciones	. Matriz de coeficientes determinante	Respuesta columna	Dx: Coeficiente determinante con respuesta-columna valores en x-.columna
2x + 1y + 1z = 3 1x – 1y – 1z = 0 1x + 2y + 1z = 0

Similarmente, Dy y Dz serían entonces: Copyright © Elizabeth Stapel 2004-2011 All Rights Reserved

Evaluando cada uno de los determinantes (con el método aquí explicado), obtenemos:









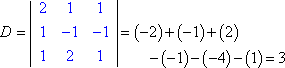
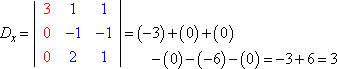
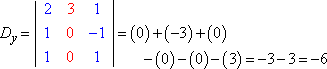
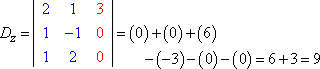
La Regla de Cramer dice que x = Dx ÷ D, y = Dy ÷ D, y z = Dz ÷ D. Es decir:

x = 3/3 = 1, y = -6/3 = -2, y z = 9/3 = 3

Eso es todo lo que dice la Regla de Cramer. Para encontrar la variable que quieras (llámala «ß» o «beta»), sólo tienes que evaluar el cociente del determinante Dß ÷ D. (Por favor, no me pidas que te explique por qué funciona esto. Sólo confía en mí que los determinantes pueden hacer muchos tipos de magia.)

• Dado el siguiente sistema de ecuaciones, encuentra el valor de z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Para resolver sólo para z, primero encuentro el determinante del coeficiente.



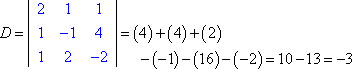
Luego formaré Dz sustituyendo la tercera columna de valores por la columna de la respuesta:

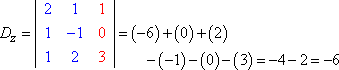
A continuación formamos el cociente y simplificamos:

z = 2

El punto de la Regla de Cramer es que no tienes que resolver todo el sistema para obtener el único valor que necesitas. Esto me ahorró bastante tiempo en algunos exámenes de física. No recuerdo en qué estábamos trabajando (algo con cables y corrientes, creo), pero la regla de Cramer fue mucho más rápida que cualquier otro método de solución (y Dios sabe que necesitaba el tiempo extra). No dejes que todos los subíndices y demás te confundan; la Regla es realmente muy sencilla. Sólo tienes que elegir la variable que quieres resolver, sustituir la columna de valores de esa variable en el determinante del coeficiente por los valores de la columna de la respuesta, evaluar ese determinante y dividir por el determinante del coeficiente. Eso es todo.

Casi.

¿Y si el determinante del coeficiente es cero? No se puede dividir por cero, ¿qué significa esto? No puedo entrar en los tecnicismos aquí, pero «D = 0» significa que el sistema de ecuaciones no tiene solución única. El sistema puede ser inconsistente (ninguna solución) o dependiente (una solución infinita, que puede expresarse como una solución paramétrica como «(a, a + 3, a – 4)»). En términos de la regla de Cramer, «D = 0» significa que tendrá que utilizar algún otro método (como las operaciones con filas de la matriz) para resolver el sistema. Si D = 0, no se puede utilizar la Regla de Cramer.

Top | Volver al índice

Cite este artículo como:

Stapel, Elizabeth. «La regla de Cramer». Purplemath. Disponible en https://www.purplemath.com/modules/cramers.htm. Accedido 2016