Resolver problemas del mundo real
Una lección para primer y segundo grado

Una lección para niños de primer grado
Por Chris Confer
Cuando los niños utilizan las matemáticas para resolver problemas del mundo real, aprenden que las matemáticas no son algo que se hace sólo para el profesor, sino que les ofrecen importantes herramientas para dar forma a su mundo. En esta lección, que aparece en el nuevo libro de Chris Confer Teaching Number Sense, Grade 1 (Math Solutions Publications, 2005), se pide a los niños que calculen cuántas galletas necesitan para un convite de la clase.
«¿Cuántas galletas?». Preguntó Juanita.
«Sí, eso es lo que necesitamos saber: cuántas galletas necesitamos para que cada uno pueda tener dos. Cuántos niños hay en nuestra clase?». Continué. Los niños coincidieron en que eran veintidós. Escribí «Hay 22 niños» en la pizarra. Luego añadí Si cada niño recibe 2 galletas, ¿cuántas galletas necesitamos?
«Podéis hacer dibujos o utilizar cubos o cualquier otra cosa para averiguarlo», dije. «Podéis trabajar solos o con uno o varios compañeros.»
De nuevo pregunté: «¿Cuántos niños hay en esta habitación?». Los niños respondieron: «Veintidós»
«¿Y cuántas galletas necesita cada uno?». «Dos galletas», dijeron.
«Quiero que cada uno de vosotros muestre su respuesta y cómo la ha calculado en un papel», continué. «Utilizad palabras, números y dibujos para mostrar lo que habéis hecho.»
Alfredo empezó a dibujar figuras de palo y dos galletas al lado de cada una, pero después de dos figuras de palo, abandonó esta idea. «Es demasiado difícil», me dijo. «¿Puedo empezar de nuevo?». Dio la vuelta al papel y empezó a dibujar conjuntos de dos galletas. Cada par de galletas tenía un espacio ligeramente mayor entre él y el siguiente par.
Alejandrina, Navin y Alicia habían dibujado pares de galletas y habían rodeado los pares. Estaban contando para comprobar que tenían veintidós pares. Navin había escrito 2 1 2 1 2 1 2 . . . y estaba contando de uno en uno. «¡Cuarenta y cuatro!», dijo triunfante.
Lorena hizo puntos para sus galletas. Los pares de galletas estaban claramente separados entre sí. Las contó, dibujó algunas más y volvió a contarlas de una en una para comprobar cuántas galletas tenía.
Pasé a Sereslinda, que había hecho círculos para las galletas, todas en fila, sin espacio que separara los pares de galletas. Se paró a contar las galletas y llegó a dieciséis. Me pregunté qué haría a continuación.
Alfredo había decidido rodear sus pares de galletas. «Estas van juntas», dijo. «Son dos niños». Parecía que Alfredo había empezado a confundir lo que representaban los círculos: ¿eran galletas o niños? Decidí no intervenir y ver si era capaz de resolverlo por sí mismo. (Ver Figura 1.)

Figura 1. Aunque había rodeado los pares,
el papel de Alfredo mostraba veintidós galletas, en lugar de veintidós pares de galletas.
Sereslinda también había empezado a rodear los pares de galletas, quizás para mostrar que cada niño recibía dos galletas. Periódicamente se detenía a contar los pares de galletas. Cuando tuvo veintidós, se detuvo.
Entonces empezó a dibujar personas de palo. Hizo diez y luego comenzó a escribir números para representar a los otros niños de la clase. Sus números llegaron a veintidós, pero sólo había dibujado once figuras de palo y diez números. Sereslinda había contado mal, pero me interesaba cómo había pasado a una forma más eficiente de representar: usando números en lugar de dibujos.
Observé cómo Sereslinda empezó a comprobar que tenía suficientes pares de galletas para cada niño de la clase. Trazó líneas para conectar cada persona de palo con un par de galletas o cada número con un par de galletas. Pero esto se convirtió en una estrategia de representación poco manejable. (Véase la figura 2.) Sereslinda empezaba a sentirse frustrada. Era el momento de intervenir.
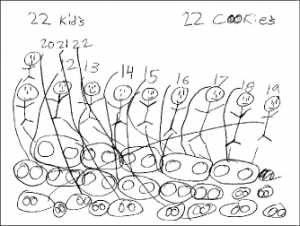
Figura 2. Sereslinda dibujó líneas para conectar sus figuras de palo
con pares de galletas. Las muchas líneas del
dibujo la confundieron, y cambió su
respuesta de cuarenta y cuatro a veintidós.
«¿Sabes qué cosa inteligente te veo hacer?». Le pregunté a Sereslinda. «Estás emparejando para comprobar que tienes dos galletas para cada persona dibujando líneas. Eso funciona muy bien para números pequeños, pero se hace difícil con números más grandes, como veintidós. ¿Puedo ofrecerte una sugerencia?» Ella asintió. «Podrías intentar señalar cada par de dos galletas y ver si cuentas veintidós pares, como si tuviéramos veintidós niños». Se lo demostré y ella siguió contando por su cuenta.
«Ya hay suficiente», me dijo. Me alegré de que esta estrategia alternativa le hubiera resultado útil.
Lorena había hecho veintidós pares de galletas y empezó a contarlas desde uno en inglés. Contó mal a mitad de camino y de alguna manera reconoció su error. «Quizá quieras contar en español», le sugerí. Cuando los niños están haciendo algo difícil, a menudo tienen más éxito cuando utilizan su primera lengua.
Lorena comenzó a contar de nuevo en español, contando desde el dos. Lo hizo varias veces, asegurándose de contar correctamente. Lorena escribió cuidadosamente 44 galletas en la parte superior de su página. (Ver Figura 3.)

Figura 3. Lorena dibujó veintidós pares de galletas y luego contó de uno en uno, en español, hasta cuarenta y cuatro.
Volví con Sereslinda. Su papel tenía veintidós pares de galletas. «¿Cuántas galletas tenemos que tener?». pregunté. Sereslinda contó los grupos de dos. «Necesitamos veintidós galletas», anunció.
«¿Entonces tenemos veintidós niños, y cada niño recibe dos galletas, y necesitamos llevar veintidós galletas?». pregunté. Sereslinda asintió y escribió 22 galletas en la parte superior de su papel.
«Tiene razón», dijo Alfredo. Pero su papel tenía una representación muy diferente: sólo veintidós galletas en lugar de veintidós pares de galletas.
Representar dos galletas por cada niño es difícil, ya que hay una cantidad de niños que es relevante y una cantidad de galletas que no coincide con el primer número, sino que representa una duplicación de ese número. Después de representar estas cantidades diferentes, los niños tienen que recordar e interpretar cuál es cuál.
Después de un rato, reuní a los niños en la alfombra y pregunté: «¿Cuántas galletas tengo que traer si sois veintidós y cada uno necesita dos galletas?». Le pedí a Alfredo que compartiera primero.
«Aquí hay dos niños», dijo Alfredo, señalando los dos círculos punteados que había dibujado para representar las galletas. «Y dos niños aquí y dos niños aquí. Y eso hace uno, dos, tres, cuatro, cinco, seis, siete, ocho, nueve, diez, once, doce, trece, catorce, quince, dieciséis, diecisiete, dieciocho, diecinueve, veinte, veintiuno, veintidós. Y hay veintidós niños y veintidós galletas.»
«¿Cuántos estáis de acuerdo en que necesitamos veintidós galletas?». Pregunté. Aproximadamente un tercio de los niños levantó la mano. Escribí veintidós galletas en la pizarra.
Le pedí a Lorena que compartiera a continuación.
«Tenemos que ver los veintidós niños y contar las galletas», dijo Lorena, señalando los pares de galletas que había dibujado. «Son uno, dos, tres, cuatro…». Contó hasta cuarenta y cuatro, reconociendo que cada pareja estaba formada por dos galletas.
«No», dijo Alfredo. «Son veintidós»
«Vamos a ver lo que ha dibujado Lorena. Dónde están los niños?». Le pregunté. Ella señaló cada par de galletas, diciendo: «Esta es para mí y esta es para Sereslinda y esta es para Heriberto . . . «
«Dejaste un espacio entre cada una para mostrar que el siguiente par de galletas era para una persona diferente. Y luego contaste todas las galletas?». pregunté. Lorena asintió. Contamos todas las galletas que Lorena había dibujado y llegamos a cuarenta y cuatro. Escribí 44 galletas en la pizarra.
«Así que no nos ponemos de acuerdo», dije al grupo. «Algunos pensáis que necesitamos veintidós galletas y otros que son cuarenta y cuatro. Cómo podemos saberlo con seguridad?»
«Dadnos las galletas», gritaron algunos niños.
«Pero yo no tengo galletas», dije. «Necesito saber cuántas traer». «Podemos usar galletas de mentira», dijo Carina.
«¿Qué podemos usar?». Pregunté. «Cubos», sugirió Heriberto.
Pasamos una bolsa de cubos alrededor del círculo, y me aseguré de que los niños recordaran con frecuencia lo que representaban los cubos. «Dos galletas para Cristina, dos galletas para Heriberto. . .
Colocamos todos los cubos en una fila, manteniendo las parejas de cubos juntas. Luego contamos los cubos desde uno. Terminamos con cuarenta y cuatro. «Así que tenemos veintidós niños y cuarenta y cuatro galletas», dije. Escribí cuarenta y cuatro galletas en la pizarra.
«Traed cuarenta y cuatro», dijo Carina.
Al día siguiente traje cuarenta y cuatro galletas y los niños estaban encantados de recibir dos cada uno.
iv