Teoremas de DeMorgan

Un matemático llamado DeMorgan desarrolló un par de reglas importantes sobre la complementación de grupos en el álgebra de Boole.

Por complementación de grupos, me refiero al complemento de un grupo de términos, representado por una barra larga sobre más de una variable.

Debería recordar del capítulo sobre puertas lógicas que invertir todas las entradas de una puerta invierte la función esencial de esa puerta de AND a OR, o viceversa, y también invierte la salida.

Así, una puerta OR con todas las entradas invertidas (una puerta Negative-OR) se comporta igual que una puerta NAND, y una puerta AND con todas las entradas invertidas (una puerta Negative-AND) se comporta igual que una puerta NOR.

Los teoremas de DeMorgan establecen la misma equivalencia en forma «inversa»: que invirtiendo la salida de cualquier puerta se obtiene la misma función que el tipo opuesto de puerta (AND vs. OR) con las entradas invertidas:

OR) con entradas invertidas:

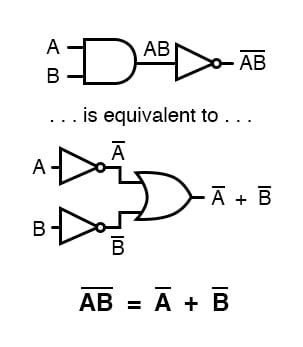
Una barra larga que se extiende sobre el término AB actúa como un símbolo de agrupación, y como tal es totalmente diferente del producto de A y B independientemente invertido.

En otras palabras, (AB)’ no es igual a A’B’. Dado que el símbolo «primo» (‘) no puede extenderse sobre dos variables como lo hace una barra, nos vemos obligados a utilizar paréntesis para que se aplique a todo el término AB en la frase anterior.

Una barra, sin embargo, actúa como su propio símbolo de agrupación cuando se extiende sobre más de una variable.

Esto tiene un profundo impacto en cómo se evalúan y reducen las expresiones booleanas, como veremos.

Teorema de DeMorgan

El teorema de DeMorgan puede pensarse en términos de romper un símbolo de barra larga.

Cuando se rompe una barra larga, la operación directamente debajo de la ruptura cambia de adición a multiplicación, o viceversa, y los trozos de barra rota permanecen sobre las variables individuales. Para ilustrar:

Cuando existen múltiples «capas» de barras en una expresión, sólo se puede romper una barra a la vez, y generalmente es más fácil comenzar la simplificación rompiendo primero la barra más larga (superior).

Para ilustrar, tomemos la expresión (A + (BC)’)’ y reduzcámosla usando los Teoremas de DeMorgan:

Siguiendo el consejo de romper primero la barra más larga (superior), empezaré por romper la barra que cubre toda la expresión como primer paso:

Como resultado, el circuito original se reduce a una puerta AND de tres entradas con la entrada A invertida:

Nunca debe romper más de una barra en un solo paso, como se ilustra aquí:

Por muy tentador que sea conservar los pasos y romper más de una barra a la vez, a menudo conduce a un resultado incorrecto, así que no lo haga.

Es posible reducir correctamente esta expresión rompiendo primero la barra corta, en lugar de la larga:

El resultado final es el mismo, pero se requieren más pasos en comparación con el uso del primer método, en el que se rompió primero la barra más larga.

Note cómo en el tercer paso rompimos la barra larga en dos lugares.

Esta es una operación matemática legítima, y no es lo mismo que romper dos barras en un solo paso!

La prohibición de romper más de una barra en un solo paso no es una prohibición de romper una barra en más de un lugar.

Romper en más de un lugar en un solo paso está bien; romper más de una barra en un solo paso no.

Puede que se pregunte por qué se han colocado paréntesis alrededor de la subexpresión B’ + C’, teniendo en cuenta el hecho de que acabo de eliminarlos en el siguiente paso.

Hice esto para enfatizar un aspecto importante pero fácilmente descuidado del teorema de DeMorgan.

Dado que una barra larga funciona como símbolo de agrupación, las variables antes agrupadas por una barra rota deben permanecer agrupadas no sea que se pierda la precedencia adecuada (orden de operación).

En este ejemplo, realmente no importaría si me olvidara de poner paréntesis después de romper la barra corta, pero en otros casos podría ser así.

Considere este ejemplo, partiendo de una expresión diferente:

Como puede ver, mantener la agrupación que implican las barras de complementación para esta expresión es crucial para obtener la respuesta correcta.

Apliquemos los principios de los teoremas de DeMorgan a la simplificación de un circuito de compuerta:

Como siempre, nuestro primer paso para simplificar este circuito debe ser generar una expresión booleana equivalente.

Podemos hacerlo colocando una etiqueta de subexpresión a la salida de cada compuerta, a medida que se conocen las entradas. Este es el primer paso de este proceso:

A continuación, podemos etiquetar las salidas de la primera compuerta NOR y de la compuerta NAND.

Cuando se trata de compuertas de salida invertida, me resulta más fácil escribir una expresión para la salida de la compuerta sin la inversión final, con una flecha que apunte justo antes de la burbuja de inversión.

Entonces, en el cable que sale de la puerta (después de la burbuja), escribo la expresión completa y complementada.

Esto me ayuda a asegurar que no olvido una barra complementaria en la subexpresión, al obligarme a dividir la tarea de escribir la expresión en dos pasos:

Por último, escribimos una expresión (o un par de expresiones) para la última puerta NOR:

Ahora, reducimos esta expresión utilizando las identidades, propiedades, reglas y teoremas (de DeMorgan) del álgebra booleana:

El circuito de puerta equivalente para esta expresión tan simplificada es el siguiente:

REVISIÓN:

• Los Teoremas de DeMorgan describen la equivalencia entre compuertas con entradas invertidas y compuertas con salidas invertidas. En pocas palabras, una compuerta NAND es equivalente a una compuerta Negative-OR, y una compuerta NOR es equivalente a una compuerta Negative-AND.
• Cuando se «rompe» una barra de complementación en una expresión booleana, la operación directamente debajo de la ruptura (adición o multiplicación) se invierte, y los trozos de la barra rota permanecen sobre los términos respectivos.
• A menudo es más fácil abordar un problema rompiendo la barra más larga (superior) antes de romper cualquier barra debajo de ella. Nunca debe intentar romper dos barras en un solo paso!
• Las barras de complementación funcionan como símbolos de agrupación. Por lo tanto, cuando se rompe una barra, los términos que se encuentran debajo de ella deben permanecer agrupados. Se pueden colocar paréntesis alrededor de estos términos agrupados como ayuda para evitar el cambio de precedencia.