Tetraedro
Tabla de contenidos
En Cuemath creemos que las Matemáticas son una habilidad para la vida. Nuestros expertos en matemáticas se centran en el «por qué» detrás del «qué». Los estudiantes pueden explorar desde una enorme gama de hojas de trabajo interactivas, visuales, simulaciones, pruebas de práctica y más para entender un concepto en profundidad.
Reserva una clase de prueba GRATIS hoy! y experimenta la clase online en vivo de Cuemath con tu hijo.
Introducción al tetraedro
Un tetraedro es uno de los cinco sólidos platónicos.
Tiene triángulos como caras.

¿Qué es un tetraedro?
Un tetraedro es una forma tridimensional que tiene todas las caras como triángulos.
Red de un tetraedro
Hagamos una pequeña actividad.
Toma una hoja de papel.
Puedes observar dos redes distintas de un tetraedro que se muestran a continuación.
Cópialo en la hoja de papel.
Córtalo por el borde y dóblalo como se indica en la figura que se muestra a continuación.
El papel doblado forma un tetraedro.

La simulación de abajo ilustra un tetraedro en 3D.
Haz clic en la arista del tetraedro y arrástrala.
¿Qué ves?
Podrás ver las 4 caras del tetraedro mientras gira.
Un tetraedro regular tiene triángulos equiláteros como caras.
Como está hecho de triángulos equiláteros, todos los ángulos internos del tetraedro medirán \(60^\c)

Un tetraedro irregular también tiene caras triangulares pero no son equiláteras.
Los ángulos internos del tetraedro en cada plano suman \ (180^\circ\) ya que son triangulares.

A menos que un tetraedro se mencione específicamente como irregular, por defecto, se asume que todos los tetraedros son tetraedros regulares.
Propiedades del tetraedro

- Tiene 4 caras, 6 aristas y 4 vértices.
- Los cuatro vértices están igualmente alejados entre sí.
- En cada uno de sus vértices se encuentran 3 aristas.
- Tiene 6 planos de simetría.
- A diferencia de otros sólidos platónicos, un tetraedro no tiene caras paralelas.
- Un tetraedro regular tiene triángulos equiláteros para todas sus caras.
- Tetraedro, cubo, octaedro, icosaedro y dodecaedro son los únicos 5 sólidos platónicos.
- Un tetraedro es una pirámide triangular; las 4 caras de un tetraedro son triángulos.
- Un tetraedro tiene 4 caras, 6 aristas y 4 vértices.
- Se forma una nueva forma alineando la cara de un tetraedro exactamente sobre una cara triangular de la pirámide cuadrada. ¿Cuántos vértices, aristas y caras tendrá la nueva forma?
- Rody tiene una tienda de campaña con forma de tetraedro regular. El volumen de la tienda es de 100 m3 y la altura es de 6 m. ¿Cuál sería la longitud de las aristas de su tienda?
- Documento de muestra de la OMI de la clase 1
- Documento de muestra de la OMI de la clase 2
- Documento de muestra de la OMI de la clase 3
- Documento de muestra de la OMI de la clase 4
- Documento de muestra de la OMI de la clase 5
- Documento de muestra de la OMI de la clase 6
- Documento de muestra de la OMI de la clase 7
- Muestra de la OMI de la clase 8
- Muestra de la OMI de la clase 9
- Muestra de la OMI de la clase 10
- Tiene 4 caras, 6 aristas y 4 vértices.
- Los cuatro vértices están igualmente alejados entre sí.
- A diferencia de otros sólidos platónicos, el tetraedro no tiene caras paralelas.
- Un tetraedro regular tiene todas sus caras como triángulos equiláteros.
- En cada vértice de un tetraedro confluyen 3 aristas.
- Un tetraedro tiene 6 planos de simetría.
Fórmula del tetraedro
A continuación se enumeran diversas fórmulas del tetraedro.
Considera un tetraedro regular formado por triángulos equiláteros de lado \(s\).

Volumen del tetraedro:
(\text{Volumen} = \frac{s^3}{6\qrt{2}})
Superficie total de un tetraedro:
(\text{TSA} = \sqrt{3}{:s^2 \N-)
Área de una cara de un Tetraedro:
(\text{Área de una cara} = \frac {\sqrt{3}}{4}s^2 \N-)
Altura de la pendiente ‘s’ de un Tetraedro:
(\text{ altura de la inclinación} = \frac {\sqrt{3}{2}s)
Altitud ‘h’ de un Tetraedro:
(\text{ Altitud} = \frac {s\qrt{6}{3})
Usa la calculadora del tetraedro para encontrar el volumen y la superficie total.
Ingresa la longitud de las aristas en la calculadora de abajo.
Ayuda a tu hijo a obtener una mejor puntuación con el Test de Diagnóstico GRATUITO propio de Cuemath. Accede a informes detallados, planes de aprendizaje personalizados y una sesión de asesoramiento GRATUITA. Intenta el test ahora.
Ejemplos resueltos
Ejemplo 1
Dos tetraedros congruentes se pegan a lo largo de su base para formar una bipirámide triangular.
¿Cuántas caras, aristas y vértices tiene esta bipirámide?
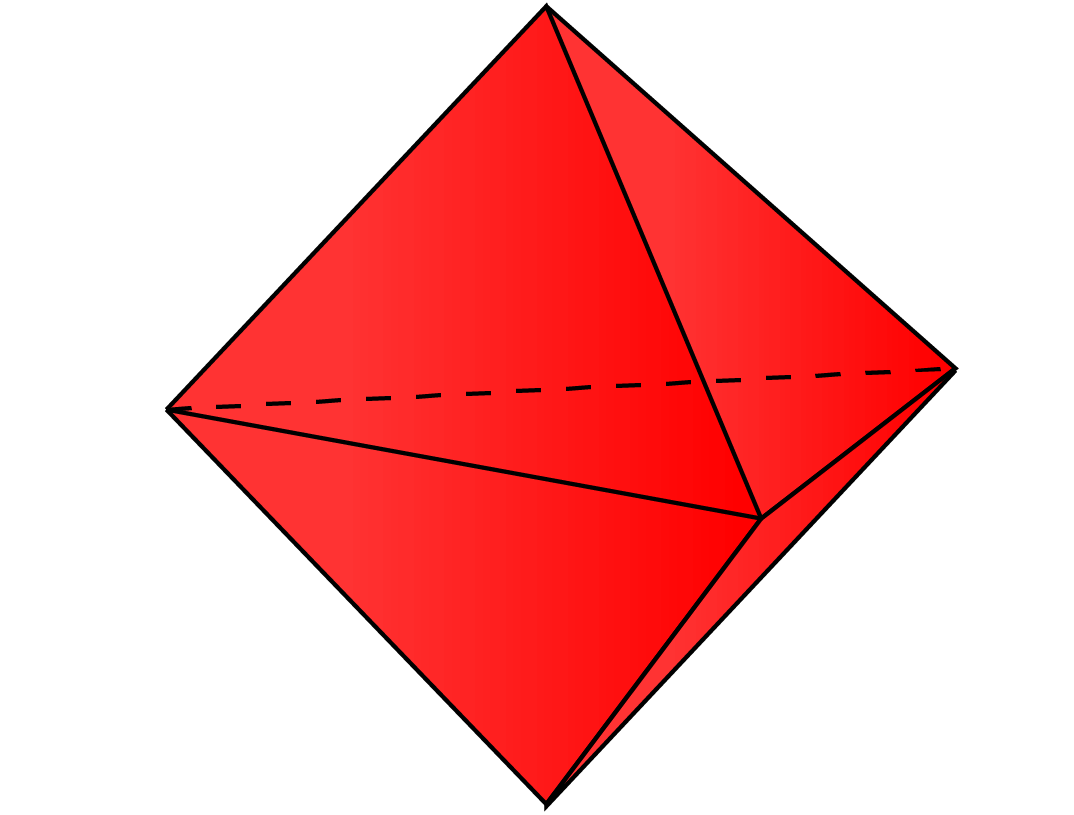
Solución:
Si abrimos la imagen anterior para ver la red de la bipirámide triangular, podemos observar que:

Hay 6 caras triangulares, 9 aristas y 5 vértices.
La bipirámide triangular tiene 6 caras triangulares, 9 aristas y 5 vértices.
Ejemplo 2
Halla el volumen de un tetraedro regular cuyo lado mide 5 unidades.
(Redondea la respuesta a 2 decimales)

Solución:
Sabemos que el volumen del tetraedro cuyo lado \N(s\) es:
(\begin{align}\text{Volumen} = \frac{s^3}{6\qrt{2}{end{align})
Sustituyendo \(s\) por 5 obtenemos
El volumen del tetraedro es de 14.73 unidades3
Ejemplo 3
Cada arista de un tetraedro regular tiene una longitud de 6 unidades.
Halla su superficie total.

Solución:
El área total de la superficie de un tetraedro regular de lado \(s\)
\(\text{TSA} = \sqrt{3} \:s^2 \N-)
Sustituyendo s = 6, obtenemos
Superficie total = 62.35 unidades2
Ejemplo 4
La suma de las longitudes de las aristas de un tetraedro regular es de 60 unidades.
Halla la superficie de una de sus caras.
Solución:
Sabemos que un tetraedro regular tiene 6 aristas.
Por tanto, la longitud de cada arista es:
(\begin{align}\frac{60}{6} = 10 \text{ units}\end{align})
Área superficial de una cara del tetraedro:
(\begin{align}\text{Área de una cara} = \frac {\sqrt{3}{4}s^2 end{align})
Sustituyendo s = 10, obtenemos:
Superficie de una de sus caras = 8.66 unidades2
Ejemplo 5
¿Para qué medida de la arista, la superficie total de un tetraedro es igual a su volumen?
Solución:
Sabemos que (\text{TSA} = \sqrt{3} \:s^2 \N) y \N(\Nque empieza{align}{texto{Volumen} = \frac{s^3}{6\\Ncuadrado{2}}{final{align})
Si TSA = Volumen, podemos decir que:
( \\Ncuadrado{3} \Nque:s^2 = \frac{s^3}{6\ctri{2}})
Resolviendo para s, tenemos
La longitud de las aristas de un tetraedro es \(6\ctr6)

¿Insuficiente en matemáticas? Comprueba cómo los profesores de CUEMATH le explican a tu hijo el tetraedro mediante simulaciones interactivas & hojas de trabajo para que nunca más tenga que memorizar nada en Matemáticas
Explora las clases online personalizadas de Cuemath Live, Interactive & para convertir a tu hijo en un experto en Matemáticas. Reserva una clase de prueba GRATIS hoy mismo!
Preguntas de práctica
Aquí tienes unas cuantas actividades para practicar.
Selecciona/escribe tu respuesta y haz clic en el botón «Comprobar respuesta» para ver el resultado.

Papeles de muestra de la Olimpiada de Matemáticas
La OIM (Olimpiada Internacional de Matemáticas) es un examen competitivo de Matemáticas que se lleva a cabo anualmente para estudiantes escolares. Anima a los niños a desarrollar sus habilidades de resolución matemática desde una perspectiva de competición.
Puedes descargar los ejemplos de exámenes de grado GRATIS desde abajo:
.
Para saber más sobre la Olimpiada de Matemáticas puedes hacer clic aquí
Preguntas frecuentes(FAQs)
¿Qué es el tetraedro?
Un tetraedro es un sólido platónico que tiene triángulos como caras.
¿Cuáles son las propiedades de un tetraedro?
Las propiedades de un tetraedro son:
¿Cuántos tetraedros hay en un cubo?
En un cubo hay 5 tetraedros.
El tetraedro del centro es regular y los demás son irregulares.

.