Comment comprendre la base (algèbre linéaire)

.

Lorsqu’on enseigne l’algèbre linéaire, le concept de base est souvent négligé. Mes étudiants en tutorat pouvaient comprendre l’indépendance linéaire et l’étendue, mais ils voyaient la base comme vous verriez un OVNI : confuse et étrangère. Et ce n’est pas bon, parce que la base agit comme un point de départ pour une grande partie de l’algèbre linéaire.

Nous avons toujours besoin d’un point de départ, d’une fondation pour construire tout le reste. Les mots ne peuvent pas être écrits sans la base d’un alphabet. Les civilisations anciennes croyaient que l’univers était formé de 4 éléments classiques – l’eau, la terre, le feu et l’air (Il y a longtemps…). Et les espaces vectoriels, le foyer naturel de l’algèbre linéaire, ont la base comme fondement.

Je vais expliquer la base de manière conceptuelle en utilisant une analogie avec la peinture. Cette analogie a été utilisée dans deux articles précédents pour expliquer deux autres concepts de l’algèbre linéaire appelés indépendance/dépendance linéaire et empan. Je vous recommande de lire ces articles en premier, car ces deux concepts reviendront plus tard.

La base des couleurs de peinture

Au lieu de faire des mathématiques, supposons que vous êtes un peintre, prêt à peindre un chef-d’œuvre sur votre toile. Tout d’abord, vous devez acheter de la peinture. Combien de couleurs devez-vous acheter ?

Bien sûr, c’est une mauvaise idée de faire une peinture en allant chez Home Depot et en achetant un pot de peinture chacun pour tous les milliers de couleurs qu’ils ont. Vous n’avez pas besoin de trente nuances de bleu différentes, du bleu azur, au bleu montagne, jusqu’au bleu victoire (idée : créer une peinture appelée « bleu défaite »). Vous avez seulement besoin d’acheter de la peinture bleue et quelques autres couleurs.

Si vous êtes un peintre avare, vous pourriez même dire que vous n’avez besoin d’acheter que 5 couleurs pour faire une peinture : rouge, jaune, bleu, blanc et noir. Bien sûr, le vert serait bien, et le rose serait cool, mais vous n’avez pas besoin d’acheter de la peinture rose et verte. Après tout, vous pouvez combiner de la peinture rouge et blanche pour faire du rose, ou de la peinture jaune et bleue pour faire du vert.

Le rouge, le jaune, le bleu, le blanc et le noir sont l’ensemble minimal de couleurs dont vous avez besoin pour faire n’importe quelle autre couleur. Nous pourrions dire que ces 5 couleurs forment une base pour l’ensemble du spectre des couleurs.

Puisque vous pouvez faire n’importe quelle autre couleur en utilisant des mélanges de ces cinq couleurs, nous pourrions dire que ces cinq couleurs couvrent l’ensemble de toutes les couleurs. De plus, chaque couleur de l’ensemble est nécessaire : vous avez besoin de peinture blanche car aucune quantité de peinture jaune, rouge, noire ou bleue mélangée ne pourra jamais créer de la peinture blanche. En d’autres termes, le rouge, le jaune, le bleu, le blanc et le noir sont indépendants les uns des autres.

Appelons votre ensemble de peintures votre palette. Pour que votre palette constitue une base pour toutes les couleurs, deux conditions doivent être vraies :

1. La palette couvre l’ensemble de toutes les couleurs.
2. Toutes les couleurs de la palette sont indépendantes les unes des autres.

Nous venons de voir que le rouge, le jaune, le bleu, le blanc et le noir remplissent ces deux conditions. En revanche, voici des exemples de palettes qui ne sont pas des bases:

• Rouge, bleu, blanc. Cela viole la première condition. Cet ensemble ne couvre pas toutes les couleurs. De nombreuses couleurs comme le jaune ou le vert sont impossibles à réaliser avec les couleurs de cet ensemble.
• Rouge, orange, jaune, vert, bleu, violet, blanc, noir. Ceci viole la condition 2. Ces couleurs recouvrent certes toutes les couleurs, mais elles ne sont pas indépendantes. Le violet est une combinaison de rouge et de bleu, le vert une combinaison de jaune et de bleu, et ainsi de suite.

La base d’un espace vectoriel

Les espaces vectoriels sont plus abstraits que les tableaux, mais ils utilisent la base de manière similaire. Un espace vectoriel est un ensemble de vecteurs où vous pouvez ajouter des vecteurs ensemble et les mettre à l’échelle. Par exemple, le plan 2-D (également connu sous le nom de R²) est un espace vectoriel. C’est l’ensemble de tous les vecteurs « bidimensionnels », qui peuvent être considérés comme des vecteurs avec une coordonnée x et une coordonnée y.

De la même façon que nous avons créé une base pour l’ensemble de toutes les couleurs, nous pouvons créer un ensemble de vecteurs qui forment une base de R². Les exigences de la base sont presque les mêmes que notre base pour les couleurs.

Base : Un ensemble de n vecteurs, {v₁, v₂,…vₙ}, est une base d’un certain espace S si ces deux conditions sont vraies :

1. {v₁, v₂,…vₙ} sont linéairement indépendants.
2. {v₁, v₂,…vₙ} recouvrent l’ensemble S. En d’autres termes, Span{v₁,v₂,…vₙ}=S

Par exemple, prenez les vecteurs (0,1) et (1,0), représentés ci-dessous en vert. Ces vecteurs sont linéairement indépendants, car il n’y a aucun moyen de mettre à l’échelle (0,1) en (1,0). De plus, ces deux vecteurs s’étendent sur l’ensemble du plan 2-D, car vous pouvez réécrire tout point de l’espace 2-D comme une combinaison linéaire de (0,1) et (1,0) :

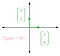
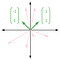
(0,1) et (1,0) forment donc une base de R² (Cette base spécifique de (0,1) et (1,0) est appelée base standard). Cependant, ce n’est pas la seule base de R² possible. Regardez les vecteurs (1,1) et (-1,1), représentés graphiquement ci-dessous. Les vecteurs roses représentent quelques combinaisons linéaires différentes :

.

Ces deux vecteurs sont également linéairement indépendants, puisqu’on ne peut pas mettre un vecteur à l’échelle de l’autre. À partir des combinaisons linéaires roses, il est également clair que (1,1) et (-1,1) couvrent la totalité de R². Par conséquent, (1,1) et (-1,1) forment une autre base pour R².

C’est un endroit où les espaces vectoriels sont très différents de l’analogie de la peinture. Avec les couleurs de la peinture, nous n’avons vraiment que la base du jaune, du bleu, du rouge, du noir et du blanc. Mais dans le monde des espaces vectoriels, tout espace a un nombre infini de bases parmi lesquelles choisir. En général, une base est le plus petit ensemble de vecteurs possible qui peut couvrir un espace. C’est l’équivalent vectoriel d’être avare avec votre peinture, et de n’acheter que les couleurs minimales dont vous avez besoin.

La base nous aide également à comprendre la structure sous-jacente d’un espace vectoriel. Par exemple, nous savons que toute base de R² sera composée d’exactement deux vecteurs, comme les deux bases que nous avons trouvées précédemment. En général :

• Pour un certain espace S, toutes les bases de S ont le même nombre de vecteurs. Ceci a été prouvé pour la première fois par Georg Hamel. Si une base de S est constituée de 4 vecteurs, alors toute base de S est constituée de 4 vecteurs.
• Une base pour un espace Rⁿ est constituée de n vecteurs. Toute base pour R³ (espace à 3 dimensions) est constituée de 3 vecteurs. Toute base pour R⁵ (espace à 5 dimensions, ne demandez pas) est constituée de 5 vecteurs.

Pourquoi la base est importante (Transformations linéaires)

En soi, la base n’a pas beaucoup d’impact. Cependant, abordons brièvement la raison pour laquelle la base est si importante pour l’algèbre linéaire.

Nous pouvons prendre un espace vectoriel et le transformer, « transformer » signifiant ici étirer, retourner ou faire tourner l’espace. Lorsque l’on travaille avec l’algèbre linéaire, transformer un espace vectoriel est aussi courant que de respirer. Supposons que je veuille transformer le graphe A en graphe B :

.

Chaque graphique a sa propre base (les vecteurs roses et bleus). Il est important de noter que le graphique A et le graphique B ne sont que deux façons différentes de représenter exactement le même espace en utilisant des bases différentes. C’est comme lire le même livre mais dans deux langues différentes, comme l’espagnol et le français.

Le passage du graphique A au graphique B est appelé une transformation linéaire du graphique. Une transformation linéaire agit comme un traducteur : Elle prend chaque point du graphique B et le déplace vers chaque point correspondant du graphique A. Elle prend le mot français et le déplace vers l’espagnol. Cependant, nous entrons maintenant dans le monde des transformations linéaires, et cela peut être expliqué une autre fois.

Conclusion

Nous avons maintenant une compréhension plus profonde de trois concepts d’algèbre linéaire : la base, l’indépendance/dépendance linéaire et l’étendue. Ces concepts sont fondamentaux pour l’algèbre linéaire. L’indépendance/dépendance linéaire vous indique quels vecteurs sont nécessaires dans un ensemble de vecteurs. La portée vous indique toutes les combinaisons possibles de vecteurs que vous pouvez créer. Et enfin, la base vous indique le plus petit ensemble de vecteurs nécessaire pour couvrir un espace vectoriel, et donc la structure de cet espace.

Maîtriser ces concepts vous donnera la base dont vous avez besoin pour comprendre concrètement l’algèbre linéaire. Après tout, une maison ne peut pas tenir sur une base branlante, et nous ne pouvons pas comprendre l’algèbre linéaire sans base. Merci de votre lecture !