Jacobien
Sous réserve d’un ensemble 
de 
équations en 
variables 
, s’écrivant explicitement comme
 |
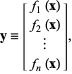(1)
|
.
ou plus explicitement comme
 |
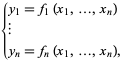(2)
|
la matrice jacobienne, parfois simplement appelée « la jacobienne » (Simon et Blume 1994) est définie par
 |
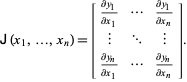(3)
|
Le déterminant de 
est le déterminant jacobien (confusément, souvent appelé aussi « le Jacobien ») et est noté
 |
(4)
|
La matrice jacobienne et le déterminant peuvent être calculés dans la déterminant peuvent être calculés dans le WolframLanguage en utilisant
JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})
Prise de la différentielle
 |
(5)
|
montre que 
est le déterminant de la matrice 
, et donne donc les rapports des volumes (contenus) à 
dimensions dans 
et 
,
 |
(6)
|
Il apparaît donc, par exemple, dans le théorème de changement de variables.
La notion de jacobien peut également être appliquée à des 
fonctions dans plus de 
variables. Par exemple, en considérant 
et 
, les Jacobiens
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
peut être défini (Kaplan 1984, p. 99).
Pour le cas de 
variables, le jacobien prend la forme particulière
 |
(9)
|
où 
est le produit scalaire et 
est le produit en croix, qui peut être développé pour donner
 |
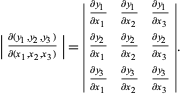(10)
|
.