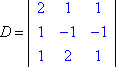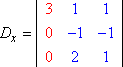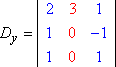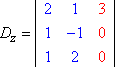Règle de Cramer

Retourner à l’index des leçons | Faire les leçons dans l’ordre | Page imprimable

Règle de Cramer

Donné un système d’équations linéaires, La règle de Cramer est un moyen pratique de résoudre une seule des variables sans avoir à résoudre tout le système d’équations. Ils n’enseignent généralement pas la règle de Cramer de cette façon, mais c’est censé être le point de la règle : au lieu de résoudre tout le système d’équations, vous pouvez utiliser la règle de Cramer pour résoudre juste une seule variable.

Utilisons le système d’équations suivant :

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

Nous avons le côté gauche du système avec les variables (la  » matrice des coefficients « ) et le côté droit avec les valeurs de réponse. Soit D le déterminant de la matrice des coefficients du système ci-dessus, et soit Dx le déterminant formé en remplaçant les valeurs de la colonne x par les valeurs de la colonne des réponses :

Similairement, Dy et Dz seraient alors : Copyright © Elizabeth Stapel 2004-2011 Tous droits réservés

En évaluant chaque déterminant (en utilisant la méthode expliquée ici), on obtient :

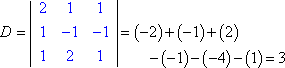
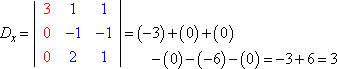
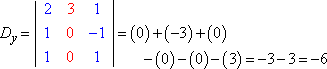
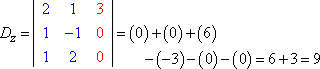
La règle de Cramer dit que x = Dx ÷ D, y = Dy ÷ D, et z = Dz ÷ D. C’est-à-dire :

x = 3/3 = 1, y = -6/3 = -2, et z = 9/3 = 3

C’est tout ce qu’il y a à dire sur la règle de Cramer. Pour trouver la variable que vous voulez (appelez-la  » ß  » ou  » bêta « ), il suffit d’évaluer le quotient du déterminant Dß ÷ D. (Ne me demandez pas d’expliquer pourquoi cela fonctionne. Faites-moi simplement confiance : les déterminants peuvent opérer plusieurs sortes de magie.)

• Étant donné le système d’équations suivant, trouvez la valeur de z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Pour résoudre uniquement z, je trouve d’abord le coefficient déterminant.

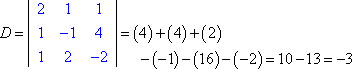
Je forme ensuite Dz en remplaçant la troisième colonne de valeurs par la colonne de réponse :

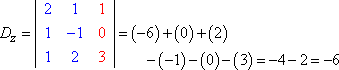
Je forme ensuite le quotient et je simplifie :

z = 2

L’intérêt de la règle de Cramer est que vous n’avez pas à résoudre tout le système pour obtenir la seule valeur dont vous avez besoin. Cela m’a fait gagner pas mal de temps lors de certains tests de physique. J’ai oublié sur quoi nous travaillions (quelque chose avec des fils et des courants, je crois), mais la règle de Cramer était tellement plus rapide que toute autre méthode de résolution (et Dieu sait que j’avais besoin de ce temps supplémentaire). Ne vous laissez pas troubler par tous ces indices et autres, la règle est vraiment très simple. Il suffit de choisir la variable que vous voulez résoudre, de remplacer la colonne de valeurs de cette variable dans le déterminant du coefficient par les valeurs de la colonne de réponse, d’évaluer ce déterminant et de diviser par le déterminant du coefficient. C’est tout ce qu’il y a à faire.

Presque.

Qu’en est-il si le déterminant du coefficient est zéro ? Vous ne pouvez pas diviser par zéro, alors qu’est-ce que cela signifie ? Je ne peux pas entrer dans les détails techniques ici, mais « D = 0 » signifie que le système d’équations n’a pas de solution unique. Le système peut être incohérent (pas de solution du tout) ou dépendant (une solution infinie, qui peut être exprimée comme une solution paramétrique telle que « (a, a + 3, a – 4) »). En termes de règle de Cramer, « D = 0 » signifie que vous devrez utiliser une autre méthode (telle que les opérations de ligne de matrice) pour résoudre le système. Si D = 0, vous ne pouvez pas utiliser la règle de Cramer.

Haut de page | Retour à l’index

.