Tétraèdre
Table des matières
Nous, à Cuemath, croyons que les mathématiques sont une compétence de vie. Nos experts en mathématiques se concentrent sur le « pourquoi » derrière le « quoi ». Les élèves peuvent explorer à partir d’une énorme gamme de feuilles de travail interactives, de visuels, de simulations, de tests pratiques et plus encore pour comprendre un concept en profondeur.
Réservez dès aujourd’hui une classe d’essai GRATUITE ! et faites l’expérience de la classe en ligne LIVE de Cuemath avec votre enfant.
Introduction au tétraèdre
Un tétraèdre est l’un des cinq solides platoniques.
Il a des triangles comme faces.

Qu’est-ce qu’un tétraèdre?
Un tétraèdre est une forme tridimensionnelle dont toutes les faces sont des triangles.
Réseau d’un tétraèdre
Faisons une petite activité.
Prenez une feuille de papier.
Vous pouvez observer deux réseaux distincts d’un tétraèdre représentés ci-dessous.
Copiez-le sur la feuille de papier.
Découpez-le le long de la bordure et pliez-le comme indiqué dans la figure présentée ci-dessous.
Le papier plié forme un tétraèdre.

La simulation ci-dessous illustre un tétraèdre en 3D.
Cliquez sur le bord du tétraèdre et faites-le glisser autour de vous.
Que voyez-vous ?
Vous allez pouvoir visualiser les 4 faces du tétraèdre lors de sa rotation.
Un tétraèdre régulier a pour faces des triangles équilatéraux.
Puisqu’il est constitué de triangles équilatéraux, tous les angles internes du tétraèdre mesureront \(60^\circ\)

Un tétraèdre irrégulier a également des faces triangulaires mais elles ne sont pas équilatérales.
Les angles internes du tétraèdre dans chaque plan s’additionnent à \(180^\circ\)car ils sont triangulaires.

Sauf si un tétraèdre est spécifiquement mentionné comme irrégulier, par défaut, tous les tétraèdres sont supposés être des tétraèdres réguliers.
Propriétés du tétraèdre

- Il possède 4 faces, 6 arêtes et 4 coins.
- Les quatre sommets sont tous également distants les uns des autres.
- A chacun de ses sommets, 3 arêtes se rencontrent.
- Il possède 6 plans de symétrie.
- Contrairement aux autres solides platoniques, un tétraèdre n’a pas de faces parallèles.
- Un tétraèdre régulier a des triangles équilatéraux pour toutes ses faces.
Formule du tétraèdre
Diverses formules du tétraèdre sont énumérées ci-dessous.
Considérez un tétraèdre régulier constitué de triangles équilatéraux de côté \(s\).

Volume du tétraèdre:
\(\text{Volume} = \frac{s^3}{6\sqrt{2}}\)
Surface totale d’un tétraèdre:
\(\text{TSA} = \sqrt{3} \ :s^2 \)
Aire d’une face d’un tétraèdre:
\(\text{Aire d’une face } = \frac {\sqrt{3}{4}s^2 \)
Hauteur de la pente ‘s’ d’un tétraèdre :
\(\text{ Hauteur oblique} = \frac {\sqrt{3}}{2}s\)
Altitude ‘h’ d’un Tétraèdre :
\(\text{ Altitude} = \frac {s\sqrt{6}}{3}\)
Utiliser la calculatrice du tétraèdre pour trouver le volume et la surface totale.
Entrez la longueur des arêtes dans la calculatrice ci-dessous.
Aidez votre enfant à obtenir de meilleurs résultats avec le test de diagnostic GRATUIT exclusif de Cuemath. Accédez à des rapports détaillés, à des plans d’apprentissage personnalisés et à une séance de conseil GRATUITE. Tentez le test maintenant.
Exemples résolus
Exemple 1
Deux tétraèdres congruents sont collés ensemble le long de sa base pour former une bipyramide triangulaire.
Combien de faces, d’arêtes et de sommets possède cette bipyramide ?
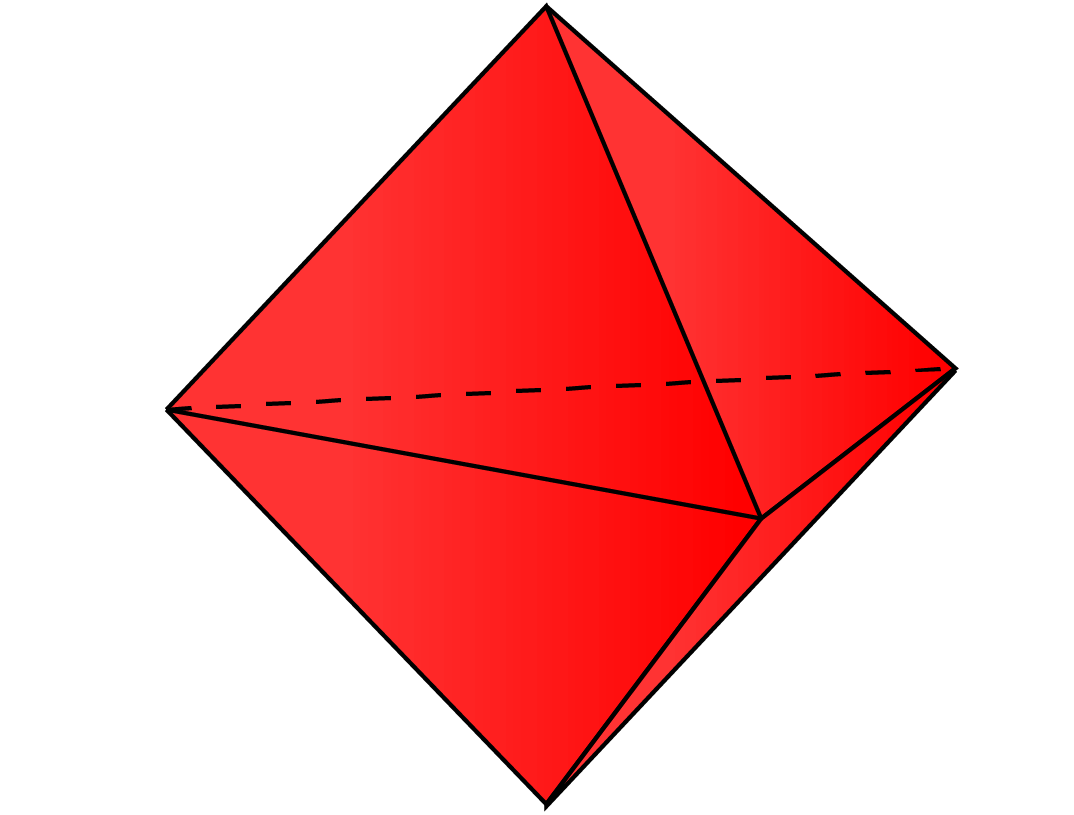
Solution:
Si nous ouvrons l’image ci-dessus pour voir le filet de la bipyramide triangulaire, nous pouvons observer que :

Il y a 6 faces triangulaires, 9 arêtes et 5 sommets.
La bipyramide triangulaire a 6 faces triangulaires, 9 arêtes et 5 sommets.
Exemple 2
Trouve le volume d’un tétraèdre régulier dont la longueur des côtés mesure 5 unités.
(Arrondissez la réponse à 2 décimales)

Solution:
Nous savons que le volume du tétraèdre dont le côté \(s\) est :
\(\begin{align}\text{Volume} = \frac{s^3}{6{sqrt{2}}\end{align}\)
En substituant \(s\) comme 5 on obtient
\
Le volume du tétraèdre est de 14.73 unités3
Exemple 3
Chaque arête d’un tétraèdre régulier est de longueur 6 unités.
Déterminez sa surface totale.

Solution :
La surface totale d’un tétraèdre régulier de côté \(s\)
\(\text{TSA} = \sqrt{3} \ :s^2 \)
Substituant s = 6, on obtient
\
Surface totale = 62.35 unités2
Exemple 4
La somme des longueurs des arêtes d’un tétraèdre régulier est de 60 unités.
Trouvez la surface d’une de ses faces.
Solution:
Nous savons qu’un tétraèdre régulier possède 6 arêtes.
Par conséquent, la longueur de chaque arête est :
\(\begin{align}\frac{60}{6} = 10 \text{ unités}\end{align}\)
Surface d’une face du tétraèdre :
\(\begin{align}\text{Aire d’une face } = \frac {\sqrt{3}}{4}s^2 \end{align}\)
Substituant s = 10, on obtient :
\
Aire de surface d’une de ses faces = 8.66 unités2
Exemple 5
Pour quelle mesure de l’arête, la surface totale d’un tétraèdre est égale à son volume ?
Solution:
Nous savons que \(\text{TSA} = \sqrt{3} \ :s^2 \) et \(\begin{align}\text{Volume} = \frac{s^3}{6\sqrt{2}}\end{align}\)
Si TSA = Volume, on peut dire que:
\( \sqrt{3} \ :s^2 = \frac{s^3}{6\sqrt{2}}\)
Solvant pour s, on a
\N
La longueur des arêtes d’un tétraèdre est \(6\sqrt6\)

- Tétraèdre, cube, octaèdre, icosaèdre et dodécaèdre sont les 5 seuls solides platoniciens.
- Un tétraèdre est une pyramide triangulaire ; les 4 faces d’un tétraèdre sont des triangles.
- Un tétraèdre a 4 faces, 6 arêtes et 4 coins.
Moins de maths ? Découvrez comment les enseignants de CUEMATH expliqueront le tétraèdre à votre enfant à l’aide de simulations interactives & feuilles de travail pour qu’il n’ait plus jamais à mémoriser quoi que ce soit en mathématiques !
Explorez Cuemath Live, Interactive & Cours en ligne personnalisés pour faire de votre enfant un expert en mathématiques. Réservez un cours d’essai GRATUIT dès aujourd’hui !
Questions d’entraînement
Voici quelques activités pour vous entraîner.
Sélectionnez/Tapez votre réponse et cliquez sur le bouton « Vérifier la réponse » pour voir le résultat.

- Une nouvelle forme est formée en alignant la face d’un tétraèdre exactement sur une face triangulaire de la pyramide carrée. Combien de sommets, d’arêtes et de faces aura la nouvelle forme ?
- Rody a une tente qui a la forme d’un tétraèdre régulier. Le volume de la tente est de 100 m3 et la hauteur est de 6 m. Quelle serait la longueur d’arête de sa tente ?
Maths Olympiad Sample Papers
L’OIM (Olympiade internationale de mathématiques) est un concours de mathématiques organisé chaque année pour les élèves des écoles. Il encourage les enfants à développer leurs compétences en résolution de problèmes mathématiques dans une perspective de compétition.
Vous pouvez télécharger les épreuves types GRATUITES par classe à partir de ci-dessous :
- Épreuve type IMO classe 1
- Épreuve type IMO classe 2
- Épreuve type IMO classe 3
- Épreuve type IMO classe 4
- Épreuve type IMO classe 5
- Épreuve type IMO classe 6
- Épreuve type IMO classe 7
- IMO Sample Paper Class 8
- IMO Sample Paper Class 9
- IMO Sample Paper Class 10
.
Pour en savoir plus sur les Olympiades de mathématiques, vous pouvez cliquer ici
Frequently Asked Questions(FAQs)
Qu’est-ce que le tétraèdre ?
Un tétraèdre est un solide platonique ayant pour faces des triangles.
Quelles sont les propriétés d’un tétraèdre ?
Les propriétés d’un tétraèdre sont :
- Il possède 4 faces, 6 arêtes et 4 coins.
- Les quatre sommets sont également distants les uns des autres.
- Contrairement aux autres solides platoniques, le tétraèdre n’a pas de faces parallèles.
- Un tétraèdre régulier a toutes ses faces sous forme de triangles équilatéraux.
- A chaque sommet d’un tétraèdre, 3 arêtes se rencontrent.
- Un tétraèdre possède 6 plans de symétrie.
Combien de tétraèdres y a-t-il dans un cube ?
Il y a 5 tétraèdres dans un cube.
Le tétraèdre central est régulier et les autres sont irréguliers.

.