12.4: Tecniche di conversione digitale-analogica
Il convertitore digitale-analogico di base è poco più di un amplificatore a somma pesata. Ogni bit successivo nella parola digitale rappresenta un livello che è il doppio del bit precedente. Se ogni bit è preso come una data corrente o tensione, i livelli crescenti possono essere prodotti usando diversi guadagni negli ingressi di somma. Un semplice convertitore a quattro bit è mostrato nella Figura \(\PageIndex{1}\).
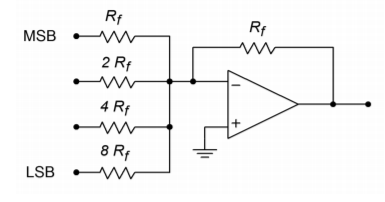
Figura \(\PageIndex{1}\: Un semplice convertitore a 4 bit.
Questo sistema può rappresentare \(2^4\), o 16, livelli diversi. Ogni ingresso è guidato da un semplice livello logico alto/basso che rappresenta un 1 o 0 per quel particolare bit. Nota che le resistenze d’ingresso variano per fattori di 2. Il guadagno per il percorso più alto è \(R_f/R_f\), o l’unità. Questo ingresso è usato per il bit più significativo della parola d’ingresso (MSB). L’ingresso successivo mostra un guadagno di \(R_f / (2R_f)\), o 0.5. Il terzo ingresso mostra un guadagno di 0,25, e l’ultimo ingresso mostra un guadagno di 0,125. L’ingresso finale ha il guadagno più basso ed è usato per il bit meno significativo della parola d’ingresso (LSB). Se la parola d’ingresso avesse una risoluzione più alta (cioè più bit), verrebbero aggiunti altri canali, ognuno dei quali avrebbe metà del guadagno dell’ingresso precedente. Per capire meglio il processo di conversione, diamo un’occhiata ad alcuni ingressi e uscite rappresentativi.
Il circuito di Figura \(\PageIndex{1}}) può essere guidato da semplici circuiti logici di tipo TTL a 5 V. 5 V rappresenta un alto logico, mentre 0 V rappresenta un basso logico. Qual è il livello di uscita se la parola d’ingresso è 0100? Poiché un alto logico rappresenta 5 V, 5 V viene applicato al secondo ingresso. Tutti gli altri ingressi ricevono un basso logico, o 0 V. L’uscita è la somma dei segnali di ingresso (ricordate, questa è un’estate invertente, quindi l’uscita finale dovrebbe avere il suo segno invertito).
Quindi, un valore di 4 (binario 100) equivale a un potenziale di 2,5 V. Se aumentiamo il valore della parola a 9 (binario 1001), vediamo
\
L’uscita minima avviene al binario 0000, (0 V) e la massima al binario 1111 (-9,375 V). La dimensione del passo è uguale al livello logico per il guadagno minimo; in questo caso è 0,625 V. Notate che il valore di uscita può essere trovato semplicemente moltiplicando il valore della parola d’ingresso per la dimensione minima del passo. Inoltre, è importante notare che il segnale di uscita è unipolare (in questo esempio, sempre negativo).
Una rappresentazione digitale, naturalmente, è costituita da una sequenza di parole, non una sola parola. In realtà, i circuiti logici alimentano costantemente l’amplificatore sommatore con nuove parole a un ritmo predeterminato. A causa del cambiamento degli ingressi, anche l’uscita del convertitore cambia costantemente. Usando i nostri valori calcolati in precedenza, se il convertitore viene alimentato con la sequenza \(0000, 0100, 1001, 1111,\) l’uscita passerà da 0 V a -2,5 V, a -5.625 V, ad un valore finale di -9.375 V. Questa uscita è rappresentata graficamente nella figura \(\PageIndex{2}\).
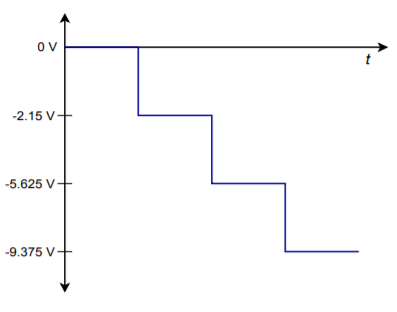
Figura \(\PageIndex{2}\: Uscita con quattro parole digitali.
Se questa sequenza viene ripetuta più e più volte, il risultato è la forma d’onda di Figura \(\PageIndex{3}). Notate che viene creata un’onda di tipo “stair-step”. Si potrebbe anche pensare a questo come ad una forma molto approssimativa di una funzione di rampa. Una rampa migliore sarebbe prodotta se usassimo tutti i valori disponibili per la sequenza di ingresso, come in \(0000, 0001, 0010, 0011, \punti, 1111\). Per rimuovere l’offset DC negativo e rendere il segnale bipolare, tutto ciò che dobbiamo fare è passare il segnale attraverso un condensatore di accoppiamento. La frequenza di questa forma d’onda è controllata dalla velocità con cui le parole sono alimentate al convertitore. Notate che aumentando la risoluzione e il numero di parole alimentate al convertitore per ciclo, si può ottenere un’approssimazione molto vicina alla funzione di rampa ideale. Cambiando le parole in ingresso con altre sequenze, possiamo creare un’ampia varietà di forme d’onda in uscita. Questo è il concetto dietro il generatore di funzioni arbitrarie digitali. Un generatore di funzioni arbitrarie permette di creare forme d’onda al di là del semplice seno/quadrato/triangolo che si trova sul tipico generatore di funzioni da laboratorio. Daremo un’occhiata più da vicino a questa particolare attrezzatura di test un po’ più tardi.
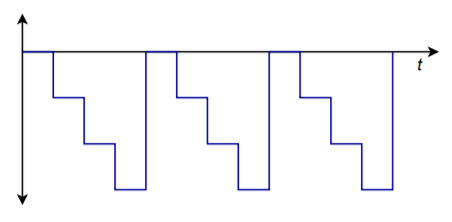
Figura \(\PageIndex{3}): Uscita ciclica.
Per aumentare la risoluzione, sembra che tutto quello che bisogna fare all’amplificatore sommatore sia aggiungere canali extra con resistenze sempre più grandi. Sfortunatamente, le dimensioni delle resistenze diventano presto impraticabili ed è necessario un altro approccio. Per esempio, un sistema a 16 bit richiederebbe che la resistenza LSB sia uguale a 65.536 \(R_f\). Un problema è che la piccola corrente d’ingresso risultante può essere nanizzata dalle correnti di bias d’ingresso e di offset. Inoltre, un’alta precisione dei componenti è necessaria per gli ingressi più significativi in termini di resistenze d’ingresso e segnali di pilotaggio. Le resistenze troppo grandi possono anche contribuire al rumore aggiunto. La soluzione standard a questo problema prevede l’uso di una rete divisore resistivo \(R/2R\).
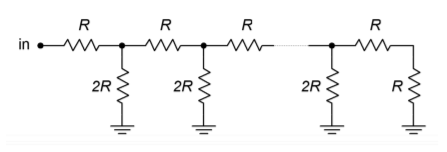
Figura \(\PageIndex{4}): \Rete ladder (R/2R)
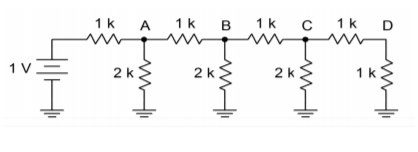
Figura \(\PageIndex{5}): Una scala a 4 stadi.
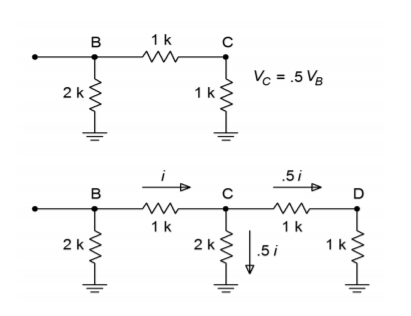
Figura \(\PageIndex{6}): Analisi ladder. a. Circuito equivalente (in alto). b. Divisione della corrente (in basso).
Se si guarda la sezione del circuito equivalente della figura \(\PageIndex{6}}), si noterà che questa porzione ora assomiglia esattamente alla porzione finale della rete originale. Cioè, ogni volta che una sezione viene semplificata e analizzata, il risultato sarà un dimezzamento della tensione e della corrente. È già evidente che la tensione a \(D) deve essere la metà della tensione a \(C), che a sua volta, deve essere la metà della tensione a \(B). Come si può ora dimostrare, ne segue che la tensione in \(B\) deve essere la metà della tensione in \(A\). In modo simile, la corrente che passa attraverso ogni gamba \(2R\) è la metà della corrente precedente. (Per la divisione della corrente, la sezione finale non viene usata per ricavare una corrente, poiché sarà uguale al valore della fase precedente). Il dimezzamento della corrente è proprio quello che serve per la rappresentazione binaria della parola di ingresso digitale.
Adattare la rete \(R/2R\) al convertitore DA è relativamente facile. La rete è alimentata da una fonte di corrente stabile, con ogni elemento \(2R\) che alimenta un amplificatore sommatore. In serie con ogni elemento 2R è un interruttore a stato solido, che imposta il livello logico appropriato. Questo è mostrato in figura (\PageIndex{7}), con la rete effettivamente sul suo lato. Quando un livello logico alto è presentato ad un dato bit, l’interruttore è chiuso e la corrente scorre attraverso l’elemento \2R\ e nell’amplificatore operazionale. Notate che l’estremità destra del resistore è effettivamente a terra, poiché il nodo sommatore dell’amplificatore operazionale è una massa virtuale. Se viene presentato un basso logico, l’interruttore devia la corrente a terra, bypassando l’amplificatore operazionale. In questo modo, le correnti opportunamente pesate vengono sommate e utilizzate per produrre la tensione di uscita.
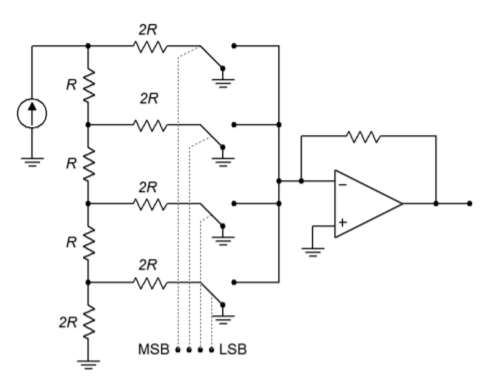
Figura \(\PageIndex{7}): Convertitore con scala R/2R.
Questa tecnica offre diversi vantaggi rispetto alla più semplice versione a guadagno ponderato. Primo, tutti i rami sono alimentati da una sorgente di corrente comune. A causa di questo, non c’è bisogno di corrispondenza del livello di uscita. Secondo, solo due diversi valori di resistenze sono richiesti per qualsiasi numero di bit usato, piuttosto che la gamma impraticabilmente ampia vista prima. È più economico controllare la tolleranza di due soli pezzi diversi piuttosto che 12 o 16. Si noti che piccole correnti d’ingresso sono ancora generate per i bit meno significativi, quindi l’attenzione alle correnti di bias d’ingresso e di offset rimane importante.
12.4.1: Limiti pratici del convertitore digitale-analogico
Forse il limite più ovvio associato al convertitore DA è la sua velocità. L’amplificatore operazionale usato nel DAC deve essere molto più veloce dei segnali finali che deve produrre. Una data forma d’onda in uscita può contenere diverse decine di punti di campionamento individuali per ciclo. L’amplificatore operazionale deve rispondere ad ogni punto di campionamento. Di conseguenza, sono richiesti un’ampia larghezza di banda e alti slew rate.
Le schede tecniche dei DAC integrati offrono alcuni parametri importanti di cui dovresti essere consapevole. Prima di tutto, c’è la velocità di conversione. Questa cifra dice quanto tempo impiega il DAC a trasformare la parola di ingresso digitale in una tensione di uscita analogica stabile. Questo stabilisce la velocità massima dei dati. Poi ci sono la precisione e la risoluzione. La risoluzione indica il numero di passi discreti che possono essere prodotti all’uscita, ed è impostata dal numero di bit disponibili. Non è la stessa cosa della precisione. La precisione è in realtà composta da diversi fattori tra cui l’errore di offset, l’errore e la non linearità. L’errore di offset è normalmente misurato applicando la parola di ingresso tutto zero e poi misurando il segnale di uscita. Idealmente, questo segnale sarà zero volt. La deviazione da zero viene presa come errore di offset. Questo ha l’effetto di rendere tutti i livelli di uscita imprecisi di una tensione costante. L’errore di offset è relativamente facile da compensare in molte applicazioni applicando un offset uguale di polarità opposta. L’errore di guadagno è una deviazione che colpisce ogni livello di uscita di una percentuale costante. È come se il segnale fosse passato attraverso un piccolo amplificatore o attenuatore. Questo errore può essere compensato utilizzando un amplificatore con un guadagno pari al reciproco dell’errore. I due guadagni si annullano efficacemente. L’effetto dell’errore di offset e di guadagno sono mostrati nelle figure \(\PageIndex{8}) e \(\PageIndex{9}).
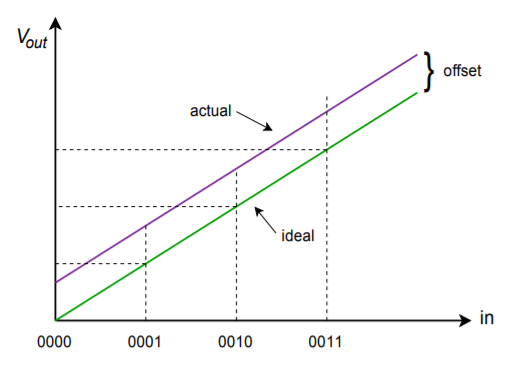
Figura \(\PageIndex{8}): Solo errore di offset.
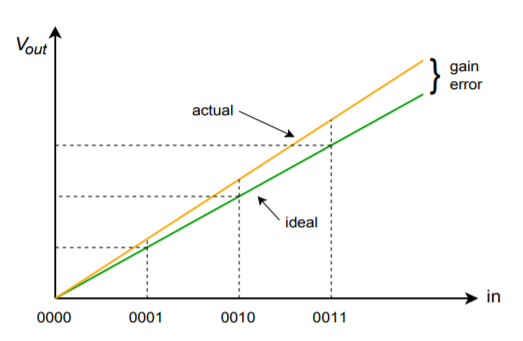
Figura \(\PageIndex{9}): Solo errore di guadagno.
Gli errori di linearità possono essere suddivisi in due forme: non linearità integrale e non linearità differenziale. La non linearità integrale dettaglia il massimo offset tra le uscite ideali e le uscite effettive per tutti i possibili ingressi. La non linearità differenziale dettaglia la massima deviazione di uscita relativa a un LSB causata da due parole di ingresso adiacenti. Se la non linearità differenziale è oltre \(\pm 1\) LSB, il sistema può essere non monotono. In altre parole, una parola di ingresso digitale più alta può effettivamente produrre una tensione di uscita analogica più bassa. Queste due forme di errore sono mostrate nella figura \(\PageIndex{10}). Si noti che è possibile avere un’alta non linearità integrale e tuttavia avere una modesta non linearità differenziale. Questo è il caso della figura \(\PageIndex{10b}).
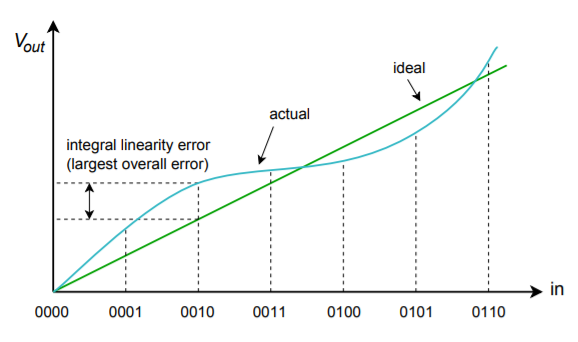
Figura \(\PageIndex{10a}): Errore di linearità Errore di linearità integrale.
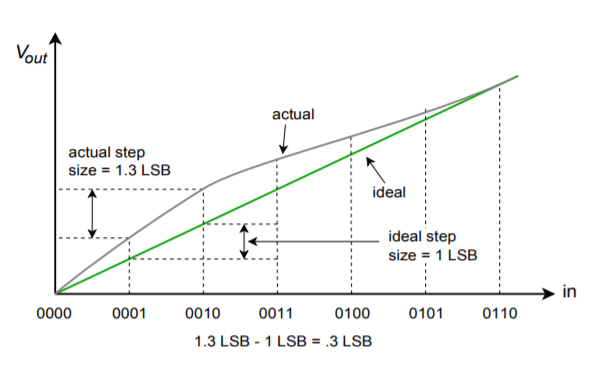
Figura \(\PageIndex{10b}): Errore di linearità (continua) Errore di linearità differenziale (errore relativo-adiacente).
Come potete vedere, la precisione dipende da fattori piuttosto complessi. Nel tentativo di ridurre il tutto a un singolo numero, alcuni produttori danno una specifica del numero effettivo di bit. Per esempio, un DAC a 16 bit può essere specificato come avente una precisione di 14 bit. Questo significa che i 14 bit più significativi si comportano in modo idealizzato, ma i 2 bit più bassi possono essere sommersi da errori di linearità. Un’altra specifica che vedrete a volte è nessun codice mancante. Questo significa che per ogni aumento della parola d’ingresso, ci sarà un appropriato cambiamento positivo del livello di uscita.
In pratica, il convertitore DA standard è usato con un filtro di uscita. Come potete vedere dalle figure precedenti, le forme d’onda prodotte dal DAC contengono un effetto collaterale a gradini. Generalmente, questo non è desiderabile. I bruschi cambiamenti nel livello di uscita indicano che sono presenti componenti a frequenza più alta. Tutte le componenti sopra il tasso di Nyquist dovrebbero essere filtrate con un appropriato filtro passa-basso. Questo filtro è a volte indicato come un filtro di ricostruzione o di lisciatura. In un sistema progettato impropriamente, il filtro di ricostruzione rimuoverà alcune delle più alte componenti di frequenza in banda (cioè le componenti immediatamente sotto la frequenza di Nyquist). Per compensare questo, i livelli logici sono spesso legati al DAC per periodi più brevi, creando così un aspetto più punteggiato, piuttosto che la forma a gradini. Questo effetto è mostrato nella Figura \(\PageIndex{11}). Anche se questa forma d’onda punteggiata sembra essere meno desiderabile della forma a gradini, crea livelli più alti per le componenti più alte, e dopo il filtraggio, il risultato è una risposta in frequenza complessiva più liscia.
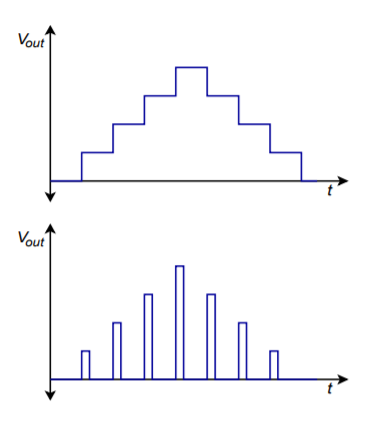
Figura \(\PageIndex{11}}): Ricostruzione dell’uscita. a. Latch a periodo completo (in alto). b. Latch a periodo parziale (in basso).
Per aumentare ulteriormente la qualità della forma d’onda di uscita, viene talvolta impiegata una tecnica nota come oversampling. L’idea di base è di creare nuovi punti di campionamento tra quelli esistenti. Il risultato è un tasso di dati molto più denso, che si spera darà risultati più precisi dopo il filtraggio. Inoltre, il più alto tasso di dati può allentare i requisiti del filtro di ricostruzione. Un sistema tipico potrebbe usare un sovracampionamento quadruplo, il che significa che la velocità dei dati in uscita è quattro volte quella originale. Quindi, per ogni parola in ingresso, devono essere aggiunte tre nuove parole. Questo effetto è mostrato nella Figura \(\PageIndex{12}).
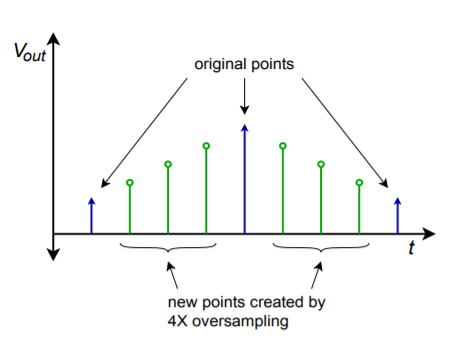
Figura \(\PageIndex{12}): Output sovracampionato.
Ci sono diversi modi per creare i nuovi punti di campionamento. Il modo più ovvio è tramite una semplice interpolazione, ma questo non raggiunge i migliori risultati. Un’altra tecnica consiste nell’inizializzare i nuovi valori a zero e poi passare il flusso di dati attraverso un filtro digitale passa-basso, che effettivamente calcola i valori corretti. Un’estensione del principio del sovracampionamento è la tecnica delta-sigma. Nel delta-sigma, tassi molto elevati di sovracampionamento sono utilizzati in combinazione con algoritmi di filtro digitale specializzati. Gli algoritmi essenzialmente scambiano la maggiore velocità dei dati con una velocità più lenta con una maggiore risoluzione. La progettazione e l’analisi dei sistemi delta-sigma è abbastanza avanzata e va oltre lo scopo di questo testo. Basti dire che queste tecniche possono aumentare la qualità del segnale in uscita e sono ampiamente utilizzate in applicazioni come i lettori CD e DVD audio di alta qualità.
12.4.2: Circuiti integrati per convertitori digitale-analogico
Ci sono molte applicazioni possibili per i convertitori digitale-analogico, e un certo numero di chip diversi si sono evoluti per soddisfare esigenze specifiche. Generalmente, è possibile raggruppare questi in classi specifiche, come alta velocità, alta risoluzione o basso costo. Esamineremo tre tipi rappresentativi. I dispositivi che esamineremo sono il DAC0832; un’unità di base a 8 bit, il DAC7545; un’unità a 12 bit compatibile con il microprocessore, e il PCM1716; un convertitore di alta qualità a 24 bit usato nell’industria audio.
DAC0832
Questo IC è un popolare convertitore a 8 bit compatibile con il microprocessore. Il DAC0830 e il DAC0831 sono simili, ma con prestazioni un po’ ridotte. È un DAC moltiplicatore. In altre parole, il segnale di uscita è una funzione della parola di ingresso digitale e un ingresso di riferimento. In alcune applicazioni, l’ingresso di riferimento non è fisso, ma piuttosto, è un segnale di ingresso variabile. Una lista di caratteristiche e il pin-out sono mostrati in Figura \(\PageIndex{13}). Notevoli elementi sono un tempo di assestamento di solo 1 \mu\s, requisiti di bassa potenza, e alta linearità. Il DAC0832 può essere usato sia in modalità stand-alone che con un microprocessore. Le forme d’onda di commutazione sono mostrate nella Figura \(\PageIndex{14}}.

Figura \(\PageIndex{13}): DAC0832. Ristampato per gentile concessione di Texas Instrutment

Figura \(\PageIndex{14}): Forme d’onda di commutazione del DAC0832 Ristampate per gentile concessione di Texas Instrutments
Un’interessante applicazione del DAC0832 può essere trovata nella figura \(\PageIndex{15}). Fondamentalmente, questo è un filtro variabile di stato controllato digitalmente.
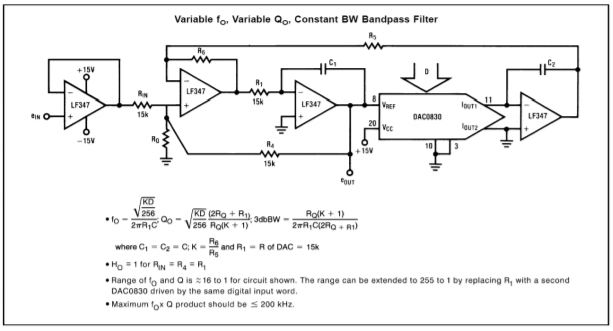
Figura \(\PageIndex{15}): Applicazione del filtro variabile di stato DAC0832. Ristampato per gentile concessione di Texas Instrutments
Nota che il convertitore sostituisce il resistore di ingresso del secondo integratore. Normalmente, quel resistore sarebbe usato per convertire la tensione di uscita del primo integratore in una corrente di ingresso per il secondo integratore. Questo lavoro è ora gestito dal DAC0832. La parola di ingresso digitale imposta effettivamente la conversione da tensione a corrente. Così, un cambiamento nella parola d’ingresso altera la frequenza di sintonizzazione del filtro proprio come un potenziometro. Confrontate questo circuito con il filtro controllato in tensione basato su OTA del capitolo undici. Concettualmente, sono molto simili.

Figura \(\PageIndex{16}): DAC7821. Ristampato per gentile concessione di Texas Instruments
DAC7821
Il DAC7821 è un convertitore lineare a 12 bit abbastanza standard ed è mostrato nella figura \(\PageIndex{16}). I suoi aspetti interessanti sono che è un convertitore moltiplicatore e che è compatibile con il microprocessore. L’effetto moltiplicatore deriva dal fatto che un riferimento è usato per guidare la rete ladder \(R/2R\). Se il riferimento viene cambiato, l’uscita viene effettivamente riscalata. Di conseguenza, puoi pensare al segnale di uscita come uguale al valore di riferimento moltiplicato per la parola di ingresso digitale. Si può anche pensare a questo come una forma di “controllo digitale del volume”.
Con l’inclusione di alcune linee logiche extra, l’IC è diventato compatibile con il microprocessore. Questo significa che il DAC7821 ha linee di chip select e di lettura/scrittura insieme alle 12 linee di ingresso dati. Questo permette al convertitore di essere collegato direttamente al bus dati del microprocessore. Usando la memoria mappata I/O, il microprocessore può scrivere dati al convertitore proprio come scrive dati nella memoria. Un sistema di microprocessore a 16 bit può presentare al convertitore tutti i dati di cui ha bisogno durante un ciclo di scrittura, tuttavia un microprocessore a 8 bit avrà bisogno di due cicli di scrittura e una qualche forma di latch. Un indirizzo può essere usato per gli 8 bit inferiori, e un altro indirizzo per i restanti 4 bit. Un sistema semplificato è mostrato nella Figura \(\PageIndex{17}) usando un microprocessore a 8 bit.
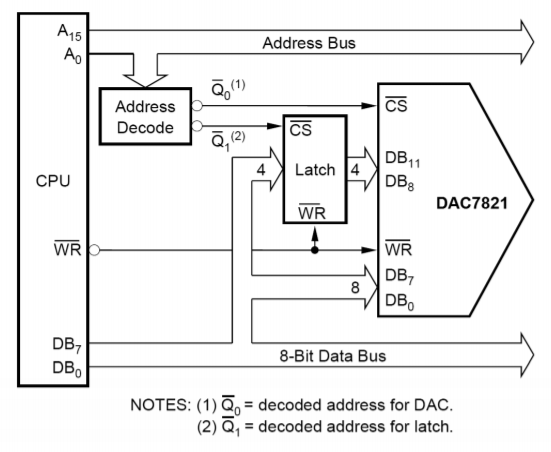
Figura \(\PageIndex{17}): Interfaccia tra microprocessore e DAC7821. Ristampato per gentile concessione di Texas Instruments
PCM5242
Il PCM5242 è un convertitore stereo a 24 bit progettato specificamente per applicazioni audio digitali di alta qualità. Viene fornito in un pacchetto VQFN (Very thin Quad Flat No-lead). Uno schema a blocchi e una lista di caratteristiche sono mostrati nella Figura \(\PageIndex{18a}). A differenza degli altri convertitori, il PCM5242 ha un ingresso dati seriale, non parallelo. Include il proprio circuito di conversione seriale a bordo e la logica. Questa tecnica aiuta a ridurre il costo del sistema. È anche sorprendentemente conveniente in quanto molti circuiti integrati specializzati nell’elaborazione di segnali digitali che potrebbero essere utilizzati con il PCM5242 utilizzano un’uscita di tipo seriale. Questa può essere alimentata direttamente nel PCM5242 in formato 16-, 24-, o 32-bit.

Figura \(\PageIndex{18a}): PCM5242. Ristampato per gentile concessione di Texas Instruments
Il foglio delle specifiche del PCM5242 è mostrato nella Figura \PageIndex{18b}. Notate che questo dispositivo è specificato con frequenze di campionamento da 48 kHz a 192 kHz. La distorsione armonica totale più il rumore è tipicamente 94 dB sotto un’uscita a fondo scala quando viene usato con una qualsiasi di queste frequenze di campionamento. A causa della sua alta risoluzione e della gamma dinamica di 114 dB, bisogna prestare molta attenzione durante il layout del circuito per evitare il ronzio e le interferenze RF.
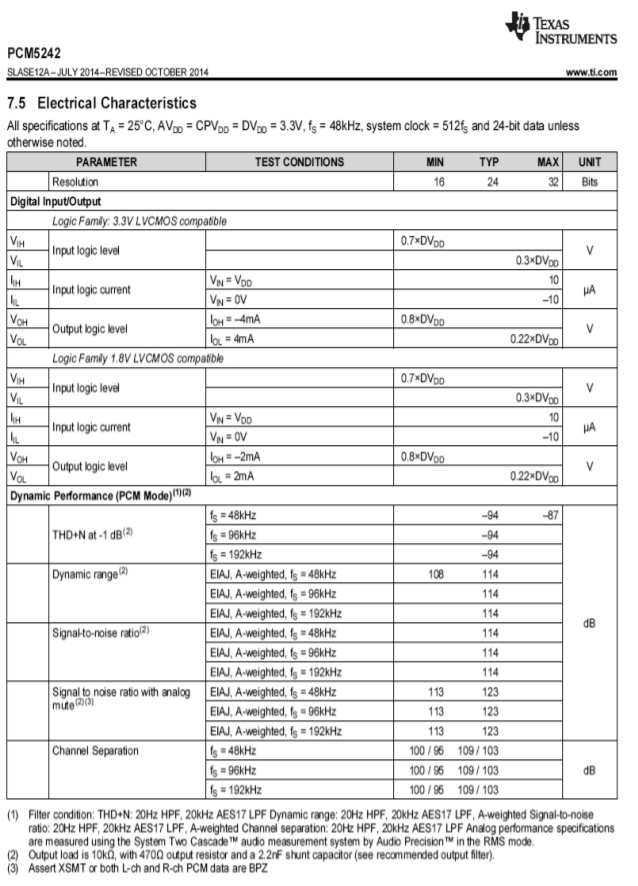
Figura \(\PageIndex{18b}): Specifiche del PCM5242. Ristampato per gentile concessione di Texas Instruments
12.4.3: Applicazioni di Circuiti Integrati di Convertitori Digitali-Analogici
Esempio (\PageIndex{1})
Forse la prima cosa a cui molte persone pensano quando sentono i termini digitale o digitalizzato, è il compact disk audio, o CD in breve. I lettori CD domestici sono esempi eccellenti dell’uso di circuiti DA di precisione nella nostra vita quotidiana. I dati musicali sono memorizzati sul CD con una risoluzione di 16 bit e una frequenza di campionamento di 44,1 kHz. Questo produce una frequenza di Nyquist di 22,05 kHz, che è abbastanza alta da comprendere il campo uditivo della maggior parte degli esseri umani. Anche la correzione degli errori e i dati ausiliari sono memorizzati sul disco. I dati sono immagazzinati sul disco sotto forma di piccolissime buche, che vengono lette da un laser. Il segnale viene poi convertito nella forma logica elettronica comune, dove viene controllato per gli errori e regolato se necessario. Il flusso di dati viene poi alimentato al convertitore DA per la ricostruzione audio. Un singolo convertitore può essere multiplexato tra i due canali stereo, o possono essere usati due convertitori dedicati. Il sovracampionamento nell’intervallo da 2X a 8X è spesso usato per migliorare la qualità del segnale. Uno schema a blocchi del sistema è mostrato in Figura \(\PageIndex{19}). La porzione di DAC attuale sembra quasi banale se confrontata con alcuni degli elementi più sofisticati.
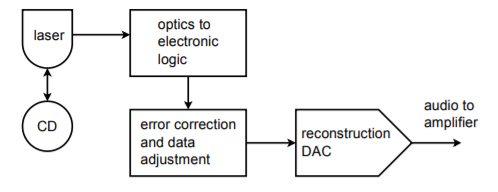
Figura \(\PageIndex{19}): Sistema di riproduzione di compact disk audio.
La densità di memorizzazione del CD ottico è piuttosto notevole. Questo piccolo disco (meno di 5 pollici di diametro) può contenere 70 minuti di musica. Ignorando i dati ausiliari, possiamo calcolare rapidamente la memoria totale. Abbiamo due canali di dati a 16 bit, o 32 bit (4 byte) per punto di campionamento. Ci sono 44.100 campioni al secondo per 70 minuti, per un totale di 185,22 megacampioni. La memorizzazione totale dei dati è di 5,927 gigabit, o 741 megabyte.
Esempio \(\PageIndex{2})
Come abbiamo già detto, è possibile collegare i DAC direttamente ai sistemi a microprocessore. Inoltre, il microprocessore può scrivere sul DAC senza più sforzo che scrivere su una posizione di memoria. Il microprocessore può scrivere qualsiasi serie di parole di dati che desideriamo sul DAC e può ripetere una sequenza praticamente all’infinito. Data questa capacità, possiamo fare un generatore di forme d’onda arbitrario. Invece di essere bloccato in una serie di forme d’onda predefinite come nei generatori di funzioni ordinarie, questo sistema permette ogni tipo di forma d’onda. L’accuratezza e la flessibilità del sistema dipenderà dalla sua velocità e dalla risoluzione DAC disponibile.
L’idea di base è quella di una tabella di look-up. Per esempio, diciamo che abbiamo un sistema a 16 bit. Creeremo una tabella di valori di dati per un ciclo della forma d’onda di uscita. Per comodità, potremmo rendere la dimensione della tabella una comoda potenza di 2, come 256. In altre parole, un singolo ciclo di uscita sarà tagliato in 256 pezzi di tempo discreto. È ovvio, quindi, che il convertitore deve essere qualche centinaio di volte più veloce della massima fondamentale che vogliamo produrre. Aumentando o diminuendo la velocità dei dati in uscita, possiamo cambiare la frequenza della fondamentale in uscita. Questa è nota come tecnica di frequenza di campionamento variabile. È anche possibile cambiare la frequenza fondamentale con una tecnica a tasso fisso (questo è un po’ più complesso, ma offre alcuni vantaggi). Un diagramma di flusso dell’uscita è mostrato nella Figura \(\PageIndex{20}).
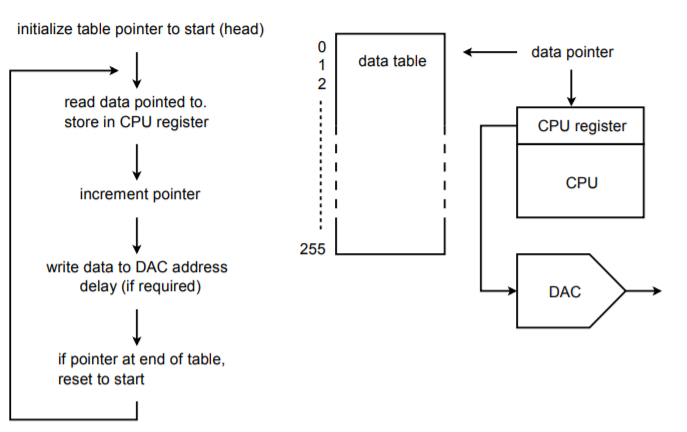
Figura \(\PageIndex{20}): Generatore di forme d’onda arbitrarie.
Al momento dell’inizializzazione, un puntatore di indirizzo è impostato all’indirizzo iniziale della tabella dati. La CPU legge i dati dalla tabella tramite il puntatore. Il puntatore viene incrementato in modo che ora punti al prossimo elemento della tabella. (Alcune CPU offrono una modalità di indirizzamento post-incremento in modo che entrambi i passi possano essere eseguiti in una singola istruzione). Successivamente, la CPU scrive i dati all’indirizzo speciale DAC. A questo punto, viene invocata una qualche forma di ritardo software/hardware che imposta la velocità dei dati in uscita. Dopo il ritardo, la CPU legge il prossimo elemento di dati tramite il puntatore e continua come nella prima esecuzione. Una volta inviato il 256° elemento, il puntatore viene riportato all’inizio della tabella e il processo continua. In questo modo, la tabella può essere pensata come circolare, o senza fine. Se il software del sistema è scritto in un linguaggio di livello superiore, la tabella puntatore/dati può essere implementata come un semplice array dove l’indice dell’array è impostato da un contatore. Questo non sarà efficiente come un approccio diretto a livello di assembly, però.
La vera bellezza di questo sistema è che la tabella dati può contenere virtualmente qualsiasi sequenza di dati. I dati potrebbero rappresentare un seno, un impulso, un triangolo o altre funzioni standard. Ancora più importante, i dati potrebbero rappresentare un’onda sinusoidale con un transitorio di rumore incorporato, o un segnale contenente una componente di ronzio altrettanto facilmente. Questi dati potrebbero provenire da tre fonti di base. In primo luogo, la tabella dei dati può essere riempita tramite calcolo diretto se l’equazione del dominio del tempo della funzione desiderata è nota. In secondo luogo, i dati potrebbero essere prodotti dall’utente attraverso qualche forma di interazione con un computer, forse con un mouse o un blocco da disegno. Infine, i dati possono essere derivati da un segnale del mondo reale. Cioè, un convertitore analogico-digitale può essere usato per registrare il segnale in forma digitale. I dati possono poi essere caricati nella tabella e riprodotti ripetutamente. Il generatore di forme d’onda arbitrarie permette all’utente di testare circuiti e sistemi con una gamma di forme d’onda che sarebbe impossibile o poco pratico generare altrimenti.
Esempio \(\PageIndex{3})
Sotto il controllo del computer, i convertitori DA possono essere utilizzati come parte di un sistema automatico di apparecchiature di prova. Per caratterizzare completamente un prodotto elettronico, è necessario eseguire una serie di test individuali. L’impostazione di ogni singolo test può richiedere molto tempo ed è soggetta all’errore dell’operatore. L’automazione di questa procedura può migliorare la ripetibilità e diminuire il tempo di prova. Ci sono molti modi in cui questo processo può essere automatizzato. Vedremo un approccio.
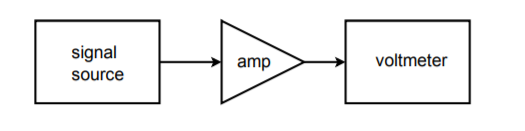
Figura \(\PageIndex{21}): Semplice configurazione di test.
Immaginiamo di voler fare delle misure di risposta in frequenza per un amplificatore a 20 frequenze diverse. Un sistema di test del circuito appropriato per questo lavoro è mostrato in Figura \(\PageIndex{21}}). Eseguire questo test manualmente richiede 20 impostazioni distinte del segnale sorgente, e 20 letture di uscita corrispondenti. Questo può rivelarsi piuttosto noioso se si devono testare molte unità. Sarebbe molto utile se ci fosse un modo in cui la frequenza della sorgente potesse essere cambiata automaticamente a valori preimpostati. Questo non è particolarmente difficile. La maggior parte delle sorgenti moderne hanno ingressi di tensione di controllo che possono essere usati per impostare la frequenza. La tensione di controllo richiesta può essere creata e impostata accuratamente attraverso l’uso di un computer e un convertitore DA. Il computer può essere programmato per inviare specifiche parole digitali al DAC, che a sua volta alimenta l’ingresso di controllo della sorgente di segnale. In altre parole, la parola dati imposta direttamente la frequenza della sorgente del segnale. Il computer può essere programmato per inviare virtualmente qualsiasi sequenza di parole di dati a quasi qualsiasi frequenza e fare tutto questo senza l’intervento dell’operatore. Tutto ciò che l’operatore deve fare è avviare il processo. La ripetibilità del test è molto alta con un sistema come questo. Uno schema a blocchi di questo sistema è mostrato nella Figura \(\PageIndex{22}}).
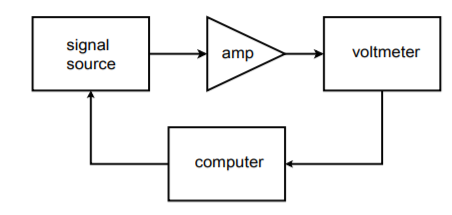
Figura \(\PageIndex{22}): Impostazione automatica del test.
Per registrare i dati, il voltmetro può essere collegato a un registratore a nastro, o meglio ancora, al computer. I dati possono essere inviati al computer in forma digitale se il voltmetro è di concezione abbastanza avanzata, oppure, con l’inclusione di un convertitore analogico-digitale, il segnale di uscita può essere direttamente campionato e manipolato dal computer. In entrambi i casi, i file di dati possono essere creati per ogni unità testata e memorizzati per un uso successivo. Inoltre, l’analisi statistica conveniente può essere eseguita rapidamente alla fine di un lotto di test. Si noti che poiché il convertitore DA genera solo un segnale di controllo, normalmente non è richiesta una risoluzione molto alta e una bassa distorsione. Se si usa un convertitore ad alta risoluzione, è possibile creare i segnali di prova nel computer (come nel generatore di funzioni arbitrarie), e fare a meno della sorgente di segnale.
Il sistema di prova automatizzato è solo una possibile applicazione del controllo degli strumenti. Un altro esempio interessante è la generazione di “spettacoli di luce” al laser. Uno schema a blocchi di un sistema semplificato è mostrato nella Figura \(\PageIndex{23}). Per creare i complessi modelli visti dal pubblico, un raggio laser viene fatto rimbalzare su piccoli specchi in movimento. Gli specchi possono essere montati su qualcosa di semplice come un galvanometro. Il galvanometro è alimentato da un DAC. Il modello che il raggio laser fa dipende da come il galvanometro muove lo specchio, che è a sua volta controllato dalle parole di dati alimentate al DAC. In pratica, si possono usare diversi specchi per deviare il raggio lungo tre assi.
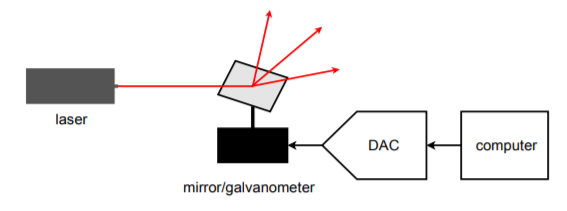
Figura \(\PageIndex{23}): Illuminazione controllata dal computer.
I convertitoriDA possono essere usati per regolare qualsiasi dispositivo con un ingresso di tipo control-voltage. Inoltre, possono essere usati per controllare dispositivi elettromeccanici che rispondono a una tensione applicata. Il loro vero vantaggio è la ripetibilità e la flessibilità che offrono.