Jacobiano
Dato un insieme 
di 
equazioni in 
variabili 
, scritto esplicitamente come
 |
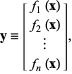(1)
|
o più esplicitamente come
 |
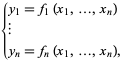(2)
|
la matrice Jacobian, talvolta chiamata semplicemente “la Jacobiana” (Simon e Blume 1994) è definita da
 |
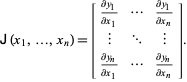(3)
|
Il determinante di 
è il determinante Jacoano (confusamente, spesso chiamato anche “il Jacobiano”) ed è indicato
 |
(4)
|
La matrice Jacobiana e determinante possono essere calcolati nel linguaggio Wolfram utilizzando
JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})
Prendendo il differenziale
 |
(5)
|
mostra che 
è il determinante della matrice 
, e quindi dà i rapporti dei volumi 
-dimensionali (contenuti) in 
e 
,
 |
(6)
|
Appare quindi, per esempio, nel teorema del cambio di variabili.
Il concetto di Jacobiano può essere applicato anche a 
funzioni in più di 
variabili. Per esempio, considerando 
e 
, i Jacobiani
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
può essere definito (Kaplan 1984, p. 99).
Per il caso di 
variabili, la Jacobiana assume la forma speciale
 |
(9)
|
dove 
è il prodotto puntiforme e 
è il prodotto incrociato, che può essere espanso per dare
 |
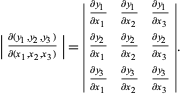(10)
|