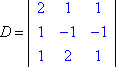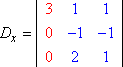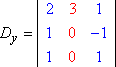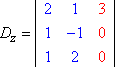Regola di Cramer

Ritorna all’indice delle lezioni | Fai le lezioni in ordine | Pagina facile da stampare

Regola di Cramer

Dato un sistema di equazioni lineari, La regola di Cramer è un modo pratico per risolvere solo una delle variabili senza dover risolvere l’intero sistema di equazioni. Di solito non si insegna la Regola di Cramer in questo modo, ma questo dovrebbe essere lo scopo della Regola: invece di risolvere l’intero sistema di equazioni, si può usare la Regola di Cramer per risolvere solo una singola variabile.

Utilizziamo il seguente sistema di equazioni:

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

Abbiamo il lato sinistro del sistema con le variabili (la “matrice dei coefficienti”) e il lato destro con i valori delle risposte. Sia D il determinante della matrice dei coefficienti del sistema di cui sopra, e sia Dx il determinante formato sostituendo i valori della colonna x con i valori della colonna delle risposte:

Similmente, Dy e Dz sarebbero allora: Copyright © Elizabeth Stapel 2004-2011 Tutti i diritti riservati

Valutando ogni determinante (usando il metodo spiegato qui), otteniamo:

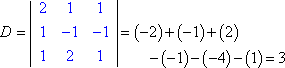
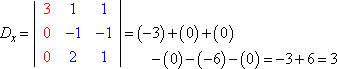
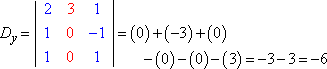
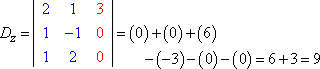
La regola di Cramer dice che x = Dx ÷ D, y = Dy ÷ D, e z = Dz ÷ D. Cioè:

x = 3/3 = 1, y = -6/3 = -2, e z = 9/3 = 3

Questo è tutto quello che c’è nella regola di Cramer. Per trovare qualsiasi variabile tu voglia (chiamala “ß” o “beta”), basta valutare il quoziente determinante Dß ÷ D. (Per favore non chiedermi di spiegare perché funziona. Fidati solo che i determinanti possono fare molti tipi di magia.

• Dato il seguente sistema di equazioni, trova il valore di z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Per risolvere solo per z, trovo prima il coefficiente determinante.

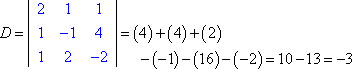
Poi formo Dz sostituendo la terza colonna di valori con la colonna delle risposte:

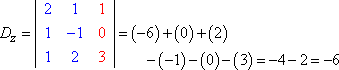
Poi formo il quoziente e semplifico:

z = 2

Il punto della Regola di Cramer è che non è necessario risolvere l’intero sistema per ottenere l’unico valore necessario. Questo mi ha fatto risparmiare una discreta quantità di tempo in alcuni test di fisica. Ho dimenticato su cosa stavamo lavorando (qualcosa con fili e correnti, credo), ma la Regola di Cramer era molto più veloce di qualsiasi altro metodo di soluzione (e Dio sa che avevo bisogno di tempo in più). Non lasciate che tutti i pedici e il resto vi confondano; la Regola è davvero molto semplice. Devi solo scegliere la variabile che vuoi risolvere, sostituire la colonna dei valori di quella variabile nel determinante del coefficiente con i valori della colonna della risposta, valutare quel determinante e dividere per il determinante del coefficiente. Questo è tutto quello che c’è da fare.

Quasi.

E se il coefficiente determinante è zero? Non si può dividere per zero, quindi cosa significa? Non posso entrare nei tecnicismi qui, ma “D = 0” significa che il sistema di equazioni non ha una soluzione unica. Il sistema può essere incoerente (nessuna soluzione) o dipendente (una soluzione infinita, che può essere espressa come una soluzione parametrica come “(a, a + 3, a – 4)”). In termini di Regola di Cramer, “D = 0” significa che dovrai usare qualche altro metodo (come le operazioni sulle righe della matrice) per risolvere il sistema. Se D = 0, non puoi usare la regola di Cramer.

Top | Return to Index