Jacobi
Gegeben eine Menge 
von 
Gleichungen in 
Variablen 
, explizit geschrieben als
 |
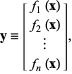(1)
|
oder expliziter als
 |
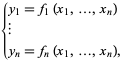(2)
|
die Jacobimatrix, manchmal einfach „die Jacobimatrix“ genannt (Simon und Blume 1994), ist definiert durch
 |
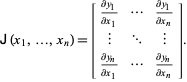(3)
|
Die Determinante von 
ist die Jacobische Determinante (verwirrenderweise, oft auch „die Jakobi“ genannt) und wird bezeichnet
 |
(4)
|
Die Jacobimatrix und Determinante können in der WolframLanguage berechnet werden mit
JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})
Das Differential
 |
(5)
|
Zeigt, dass 
die Determinante der Matrix 
ist, und gibt somit die Verhältnisse der 
-dimensionalen Volumina (Inhalte) in 
und 
an,
 |
(6)
|
Sie taucht daher zum Beispiel im Satz vom Variablenwechsel auf.
Das Konzept der Jacobi kann auch auf 
Funktionen in mehr als 
Variablen angewendet werden. Betrachten Sie zum Beispiel 
und 
, die Jacobi
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
kann definiert werden (Kaplan 1984, S. 99).
Für den Fall von 
Variablen nimmt der Jacobian die spezielle Form
 |
(9)
|
wobei 
ist das Punktprodukt und 
ist das Kreuzprodukt, was erweitert werden kann zu
 |
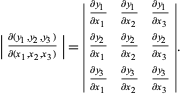(10)
|