Maximaler Wert einer ganzen Zahl: Java Vs C vs Python | Baeldung on Computer Science

Einführung

Wenn wir in der Datenwissenschaft von Ganzzahlen sprechen, meinen wir einen Datentyp, der einen Bereich von mathematischen Ganzzahlen repräsentiert. Wir wissen, dass mathematische Ganzzahlen keine Obergrenze haben, aber das könnte ein Problem in Bezug auf die Speichergröße sein, was fast jede Computerarchitektur dazu zwingt, diesen Datentyp zu begrenzen.

Das ist also die Frage, die wir heute stellen wollen: „Was ist der maximale Integer-Wert, den wir auf einer bestimmten Maschine darstellen können?“

Problemerläuterung

Nun, es gibt keine eindeutige Antwort auf diese Frage, da es viele Faktoren gibt, die die Antwort beeinflussen. Die wichtigsten sind:

Plattformbits
Verwendete Sprache
Versionen mit oder ohne Vorzeichen

In der Informatik ist die gebräuchlichste Darstellung von ganzen Zahlen durch eine Gruppe von binären Ziffern (Bits), die in einem binären Zahlensystem gespeichert werden. Die Reihenfolge der Speicherbytes variiert – mit Bits können wir Ganzzahlen codieren.

Wir können die Unterschiede in diesem einfachen Beispiel sehen: Mit Bits, können wir ganze Zahlen von bis oder von $- 2^{n-1}$ bis $2^{n-1} - 1$ kodieren.

Normalerweise wird die Integer-Größe durch die Maschinenarchitektur definiert, aber einige Computersprachen definieren Integer-Größen auch unabhängig. Verschiedene CPUs unterstützen unterschiedliche Datentypen, basierend auf ihrer eigenen Plattform. Typischerweise unterstützen alle sowohl vorzeichenbehaftete als auch vorzeichenlose Typen, aber nur mit einer begrenzten und festen Anzahl von Breiten, normalerweise 8, 16, 32 und 64 Bit.

Einige Sprachen definieren zwei oder mehr Arten von Integer-Datentypen, einen kleineren, um Speicher zu sparen und weniger Platz zu beanspruchen, und einen größeren, um den unterstützten Bereich zu erweitern.

Eine weitere Sache, die man im Auge behalten muss, ist die Wortgröße (auch Wortlänge genannt) der Plattform.

In der Informatik ist ein Wort die Einheit von Daten, die von einem bestimmten Prozessordesign verwendet wird, ein Datenstück fester Größe, das von der Hardware des Prozessors als Einheit behandelt wird. Wenn wir von Wortgröße sprechen, beziehen wir uns auf die Anzahl der Bits in einem Wort, und dies ist ein entscheidendes Merkmal einer bestimmten Computerarchitektur und eines Prozessordesigns.

Aktuelle Architekturen haben typischerweise eine Wortgröße von 64 Bit, aber es gibt auch welche mit 32 Bit.

Zeit für die Antworten

In diesem Abschnitt werden wir unsere Fragen beantworten, angefangen vom alten Freund C über das relativ neue Python bis hin zum Evergreen Java. Fangen wir an.

3.1. C

Die Sprache C wurde 1972 mit dem Ziel entwickelt, auf verschiedenen Maschinentypen gleich zu funktionieren. Sie legt also nicht direkt einen Bereich für den Integer-Datentyp fest, da dieser von der Maschinenarchitektur abhängt.

Dennoch gibt es in C zwei Arten von Integern: short und long.

Ein kurzer Integer besteht aus mindestens 16 Bit. Auf einer 16-Bit-Maschine fällt sie also mit dem Long-Integer-Format zusammen. Das kurze Ganzzahlformat reicht von -32.767 bis 32.767 für die vorzeichenbehaftete Version und von 0 bis 65.535 für die vorzeichenlose. Es ist seltsam, aber es scheint, dass für die vorzeichenbehaftete Version eine Zahl fehlt. Das ist leicht zu erklären: denn wir brauchen ein Bit für das Vorzeichen!

Wenn wir auf einem 64-Bit-System arbeiten, können wir leicht ausrechnen, dass das lange Format einen $2^{64-1}$ Wert erreichen kann, der 18 entspricht,446.744.073.709.551.615 für den vorzeichenlosen Datentyp entspricht und in der vorzeichenbehafteten Version von -9.223.372.036.854.775.807 bis 9.223.372.036.854.775.807 reicht.

Der Vollständigkeit halber machen wir noch einen kleinen Ausflug zum Datentyp long long integer. Das Long-Long-Format gibt es nicht in C, sondern nur in der C99-Version. Er hat die doppelte Speicherkapazität eines long-Datentyps, wird aber offensichtlich von Compilern, die den bisherigen C-Standard voraussetzen, nicht unterstützt. Mit dem Long-Datentyp können wir einen riesigen $2^{64-1}$ erreichen, wenn wir ihn auf einer 32-Bit-Maschine oder höher ausführen.

3.2. Java

Wenn wir über Java sprechen, müssen wir uns daran erinnern, dass es über eine virtuelle Maschine arbeitet. Das erspart uns die ganze Variabilität, die für die Sprache C erklärt wurde.

Java unterstützt nur vorzeichenbehaftete Versionen von Ganzzahlen. Diese sind:

byte (8 Bits)
short (16 Bits)
int (32 Bits)
long (64 Bits)

Mit dem Long-Integer-Format können wir also $2^{64-1}$ wie bei C auf einer 64-Bit-Maschine erreichen, diesmal aber auf jeder Maschinenarchitektur.

Mit ein paar Bitmanipulationen können wir jedoch dank des char-Formats vorzeichenlose Versionen erhalten. Das ist ein 16-Bit-Format, so dass das vorzeichenlose Integer-Format 65.535 erreichen kann.

Aber mit Java können wir mit einem kleinen Hack noch weiter gehen, so dass wir sehr große Integer-Zahlen durch die Klassenbibliothek BigInteger darstellen können. Diese Bibliothek kombiniert Arrays aus kleineren Variablen, um riesige Zahlen aufzubauen. Die einzige Grenze ist der physikalische Speicher, so dass wir einen riesigen, aber immer noch begrenzten Bereich von Ganzzahlen darstellen können.

Bei 1 Kilobyte Speicher können wir zum Beispiel Ganzzahlen mit bis zu 2.466 Stellen erreichen!

3.3. Python

Python unterstützt als Top-Level-Konstrukt direkt beliebige Präzisions-Ganzzahlen, auch Infinite-Precision-Integer oder Bignums genannt.

Das bedeutet, dass wir wie bei Java BigInteger so viel Speicher wie nötig für eine beliebig große Ganzzahl verwenden. Programmiersprachlich stellt sich diese Frage für Python also gar nicht, denn der einfache Integer-Typ ist theoretisch unbegrenzt.

Was nicht unbegrenzt ist, ist die Wortgröße des aktuellen Interpreters, die in den meisten Fällen mit der Wortgröße der Maschine übereinstimmt. Diese Information ist in Python als sys.maxsize verfügbar und ist die Größe der größtmöglichen Liste oder speicherinternen Sequenz, die dem maximalen Wert entspricht, der durch ein vorzeichenbehaftetes Wort dargestellt werden kann.

Auf einer 64-Bit-Maschine entspricht das $2^{64-1}$ = 9.223.372.036.854.775.807.

Flussdiagramm

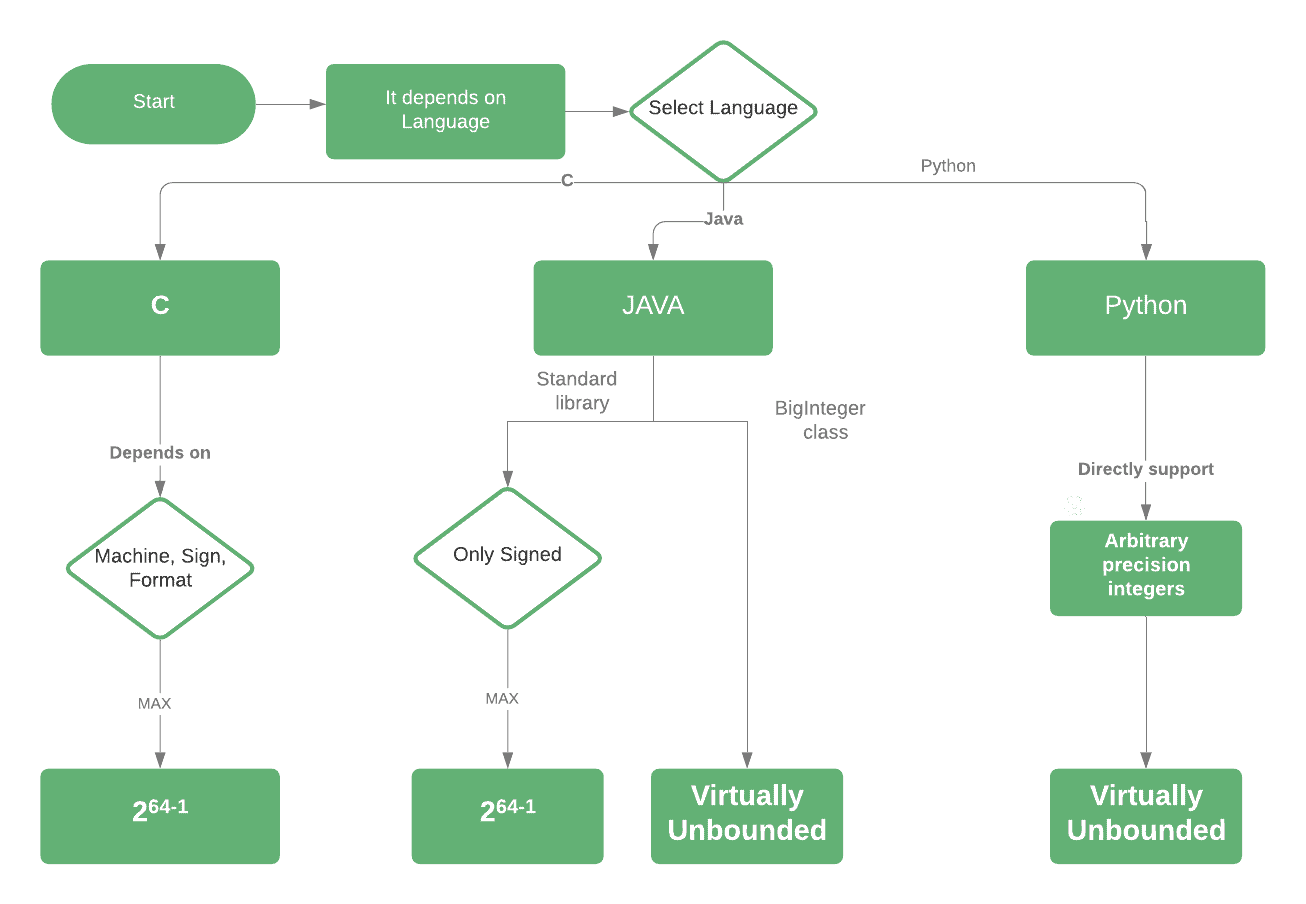
Lassen Sie uns einen Blick auf ein Flussdiagramm werfen, um zusammenzufassen, was wir bisher gesehen haben:

Realer Code für jede Sprache

Hier ist etwas echter Code, um direkt zu überprüfen, was wir bisher besprochen haben. Der Code demonstriert die maximalen und minimalen Werte von Ganzzahlen in jeder Sprache.

Da diese Werte bei Python nicht existieren, zeigt der Code, wie man die Wortgröße des aktuellen Interpreters anzeigt.

5.1. C-Code

#include<bits/stdc++.h>int main() { printf("%d\n", INT_MAX); printf("%d", INT_MIN); return 0; }

5.2. Java Code

public class Test { public static void main(String args) { System.out.println(Integer.MIN_VALUE); System.out.println(Integer.MAX_VALUE); }}

5.3. Python Code

import platformplatform.architecture()import syssys.maxsize

Abschluss

In diesem Artikel haben wir die Unterschiede zwischen diesen drei Top-Sprachen in Bezug auf die maximal mögliche Ganzzahl behandelt. Wir haben auch gezeigt, dass diese Frage in manchen Situationen nicht zutrifft.

Allerdings sollte man immer das in seiner Situation am besten passende verwenden, um Speicherverbrauch und Systemverzögerungen zu vermeiden.

Maximalwert einer ganzen Zahl: Java Vs C vs Python