12.4: Digitaal-Analoog Conversie Technieken
De basis digitaal-naar-analoog converter is weinig meer dan een gewogen sommatieversterker. Elk opeenvolgend bit in het digitale woord vertegenwoordigt een niveau dat tweemaal zo groot is als het voorgaande bit. Als elk bit wordt opgevat als een bepaalde stroom of spanning, kunnen de oplopende niveaus worden geproduceerd door verschillende versterkingen in de sommingangen te gebruiken. Een eenvoudige 4-bit omvormer is te zien in figuur
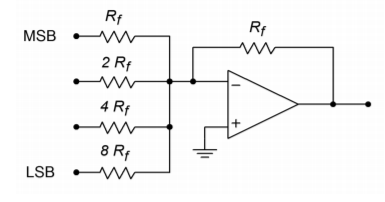
Figuur
(\PageIndex{1}\): Een eenvoudige 4-bit omzetter.
Dit systeem kan \(2^4\), of 16, verschillende niveaus weergeven. Elke ingang wordt aangestuurd door een eenvoudig hoog/laag logisch niveau dat een 1 of 0 voor dat specifieke bit voorstelt. Merk op dat de ingangsweerstanden variëren met factoren van 2. De versterking voor het hoogste pad is \(R_f/R_f\), of eenheid. Deze ingang wordt gebruikt voor het meest significante bit van het ingangswoord (MSB). De volgende ingang heeft een versterking van \(R_f / (2R_f)\), ofwel 0,5. De derde ingang heeft een versterking van 0,25, en de laatste ingang heeft een versterking van 0,125. De laatste ingang heeft de laagste versterking en wordt gebruikt voor het minst significante bit van het ingangswoord (LSB). Indien het ingangswoord een hogere resolutie had (d.w.z. meer bits), zouden extra kanalen worden toegevoegd, elk met de helft van de versterking van de voorgaande ingang. Laten we, om het conversieproces beter te begrijpen, eens kijken naar een paar representatieve ingangen en uitgangen.
De schakeling van figuur (PaginaIndex{1}) kan worden aangestuurd door eenvoudige 5 V TTL-type logische circuits. 5 V staat voor een logisch hoog, terwijl 0 V voor een logisch laag. Wat is het uitgangsniveau als het ingangswoord 0100 is? Omdat een logisch hoog 5 V vertegenwoordigt, wordt 5 V toegepast op de tweede ingang. Alle andere ingangen krijgen een logische lage waarde, ofwel 0 V. De uitgang is de som van de ingangssignalen (vergeet niet dat dit een inverterende zomer is, dus het teken van de uiteindelijke uitgang moet worden omgekeerd).
Zo komt een waarde van 4 (binair 100) overeen met een potentiaal van 2,5 V. Verhogen we de woordwaarde tot 9 (binair 1001), dan zien we
De minimale uitgang treedt op bij binair 0000, (0 V) en de maximale bij binair 1111 (-9,375 V). De stapgrootte is gelijk aan het logische niveau maal de minimum versterking; in dit geval is dat 0,625 V. Merk op dat de uitgangswaarde kan worden gevonden door eenvoudig de waarde van het ingangswoord te vermenigvuldigen met de minimale stapgrootte. Ook is het belangrijk op te merken dat het uitgangssignaal unipolair is (in dit voorbeeld altijd negatief).
Een digitale weergave bestaat natuurlijk uit een opeenvolging van woorden, niet slechts uit één woord. In werkelijkheid voeden de logische circuits de sommatieversterker voortdurend met nieuwe woorden in een vooraf bepaalde snelheid. Door de veranderende input verandert de output van de converter ook voortdurend. Als we onze eerder berekende waarden gebruiken en de converter wordt gevoed met de sequentie 0000, 0100, 1001, 1111, dan zal de uitgang van 0 V naar -2,5 V, naar -5.625 V, naar een uiteindelijke waarde van -9,375 V. Deze uitgang is grafisch weergegeven in figuur
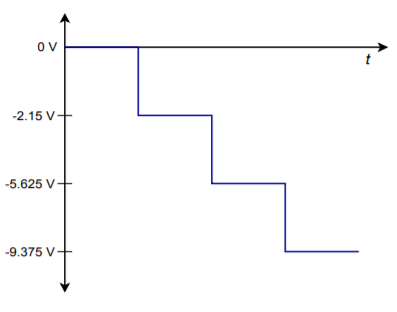
Figuur
(\PageIndex{2}\): Uitgang met vier digitale woorden.
Als deze reeks steeds wordt herhaald, is de golfvorm van figuur \(\PageIndex{3}\) het resultaat. Merk op dat er een “stair-step” type golf ontstaat. Je zou dit ook kunnen zien als een zeer ruwe vorm van een hellingsfunctie. Een betere helling zou worden verkregen als we alle beschikbare waarden voor de invoerreeks zouden gebruiken, zoals in 0000, 0001, 0010, 0011, 1111). Om de negatieve DC-offset te verwijderen en het signaal bipolair te maken, hoeven we het signaal alleen maar door een koppelcondensator te leiden. De frequentie van deze golfvorm wordt geregeld door de snelheid waarmee de woorden naar de omzetter worden gevoerd. Merk op dat door de resolutie te verhogen en het aantal woorden dat per cyclus aan de omzetter wordt toegevoerd, een zeer dichte benadering van de ideale hellingsfunctie kan worden bereikt. Door de ingangswoorden in andere reeksen te veranderen, kunnen wij een grote verscheidenheid van uitgangsgolfvormen creëren. Dit is het concept achter de digitale arbitraire functiegenerator. Met een arbitraire functiegenerator kunt u golfvormen creëren die verder gaan dan de eenvoudige sinus/vierkant/driehoek die u op de typische laboratoriumfunctiegenerator aantreft. We zullen dit specifieke stukje testapparatuur straks nader bekijken.
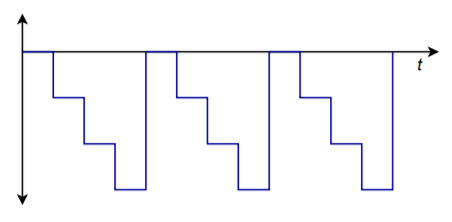
Figuurtje (Pagina-index{3}): Cycled output.
Om de resolutie te verhogen, lijkt het erop dat je alleen maar extra kanalen met steeds grotere weerstanden aan de sommeerversterker hoeft toe te voegen. Helaas worden de weerstanden al snel onpraktisch en is een andere aanpak nodig. Voor een 16-bits systeem zou bijvoorbeeld de LSB-weerstand gelijk moeten zijn aan 65.536 (R_f). Een probleem is dat de resulterende kleine ingangsstroom in de schaduw kan komen te staan van de bias- en offsetstromen van de ingang. Ook is een hoge componentnauwkeurigheid nodig voor de belangrijkere ingangen in termen van de ingangsweerstanden en de aandrijfsignalen. De te grote weerstanden kunnen ook extra ruis veroorzaken. De standaard oplossing voor dit probleem is het gebruik van een \(R/2R\) weerstandsdeler netwerk.
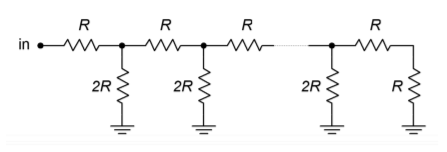
Figuur \(\PageIndex{4}\): \laddernetwerk
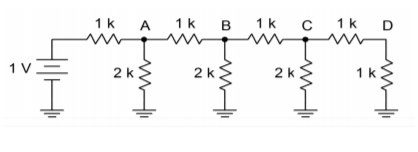
Figuur (\PageIndex{5}): Een 4-traps ladder.
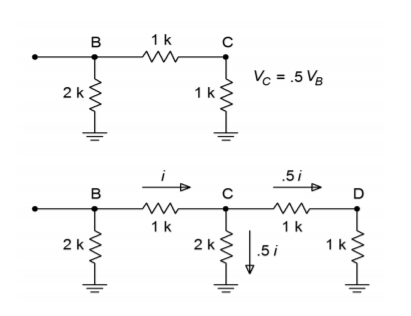
Figuur (\PageIndex{6}\): Ladderanalyse. a. Equivalente stroomkring (boven). b. Stroomverdeling (onder).
Als u naar het gedeelte met de equivalente stroomkring van figuur (PaginaIndex{6}) kijkt, zult u zien dat dit gedeelte er nu precies zo uitziet als het laatste gedeelte van het oorspronkelijke netwerk. Dat wil zeggen dat telkens wanneer een doorsnede vereenvoudigd en geanalyseerd wordt, het resultaat een halvering van spanning en stroom zal zijn. Het is al duidelijk dat de spanning op D de helft moet zijn van de spanning op C, die op zijn beurt de helft moet zijn van de spanning op B. Zoals je nu kunt bewijzen, volgt hieruit dat de spanning op \B de helft moet zijn van de spanning op \A. Op dezelfde manier is de stroom door elk pootje van \(2R) de helft van de vorige stroom. (Bij stroomdeling wordt het laatste deel niet gebruikt om een stroom af te leiden, omdat deze gelijk zal zijn aan de waarde in de voorafgaande trap). De halvering van de stroom is precies wat nodig is voor de binaire weergave van het digitale ingangswoord.
Het aanpassen van het \(R/2R\) netwerk aan de DA-omzetter is betrekkelijk eenvoudig. Het netwerk wordt gevoed door een stabiele stroombron, waarbij elk element van het \(2R\) netwerk in een somversterker komt. In serie met elk element staat een solid-state schakelaar, die het juiste logische niveau instelt. Dit is te zien in figuur 7, met het netwerk effectief op zijn kant. Wanneer een bepaalde bit een logisch hoog niveau krijgt, wordt de schakelaar gesloten en loopt er stroom door het element en naar de op-versterker. Merk op dat het rechter uiteinde van de weerstand effectief aan massa ligt, aangezien het somknooppunt van de op-versterker een virtuele massa is. Als een logisch laag wordt aangeboden, leidt de schakelaar de stroom naar massa en wordt de op-versterker genegeerd. Op deze manier worden de gewogen stromen bij elkaar opgeteld en gebruikt om de uitgangsspanning te produceren.
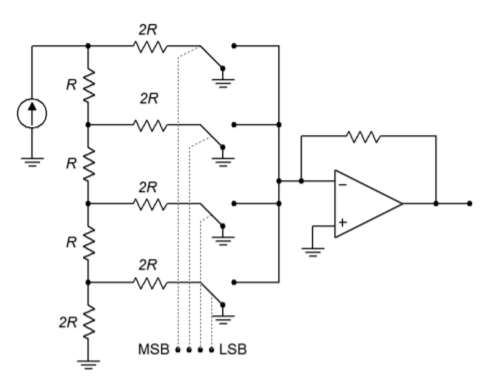
Figuurtje (Pagina-index{7}): Convertor met R/2R ladder.
Deze techniek biedt verschillende voordelen boven de eenvoudiger gewogen versterkingsversie. Ten eerste worden alle takken gevoed door één gemeenschappelijke stroombron. Hierdoor is er geen noodzaak tot aanpassing van het uitgangsniveau. Ten tweede zijn slechts twee verschillende waarden van weerstanden vereist voor om het even welk aantal gebruikte bits, in plaats van de onpraktisch brede waaier die eerder werd gezien. Het is economischer om de tolerantie van slechts twee verschillende onderdelen te controleren dan 12 of 16. Merk op dat er nog steeds kleine ingangsstromen worden gegenereerd voor de minst significante bits, dus aandacht voor ingangsbias en offsetstromen blijft belangrijk.
12.4.1: Praktische Digital-to-Analog Converter Limits
De meest voor de hand liggende limiet van de DA-converter is misschien wel zijn snelheid. De op amp die in de DAC wordt gebruikt moet veel sneller zijn dan de uiteindelijke signalen die hij moet produceren. Een gegeven uitgangsgolfvorm kan enkele tientallen individuele samplepunten per cyclus bevatten. De op-versterker moet op elk sample-punt reageren. Bijgevolg zijn een grote bandbreedte en hoge slew rates vereist.
Integrated DAC spec sheets bieden een paar belangrijke parameters waarvan u zich bewust moet zijn. Allereerst is er de conversiesnelheid. Deze geeft aan hoe lang de DAC er over doet om het digitale ingangswoord om te zetten in een stabiele analoge uitgangsspanning. Dit bepaalt de maximale datasnelheid. Vervolgens komen de nauwkeurigheid en de resolutie. De resolutie geeft het aantal discrete stappen aan dat aan de uitgang kan worden geproduceerd, en wordt bepaald door het aantal beschikbare bits. Dit is niet hetzelfde als nauwkeurigheid. Nauwkeurigheid bestaat eigenlijk uit verschillende factoren, waaronder offsetfout, fout, en niet-lineariteit. De offsetfout wordt gewoonlijk gemeten door het ingangswoord geheel nul toe te passen en vervolgens het uitgangssignaal te meten. In het ideale geval is dit signaal nul volt. De afwijking van nul wordt genomen als de offsetfout. Dit heeft tot gevolg dat alle uitgangsniveaus onnauwkeurig worden door een constante spanning. De offsetfout kan in vele toepassingen betrekkelijk gemakkelijk worden gecompenseerd door een gelijke offset van tegengestelde polariteit toe te passen. Versterkingsfout is een afwijking die elk uitgangsniveau met een constant percentage beïnvloedt. Het is alsof het signaal door een kleine versterker of verzwakker wordt geleid. Deze fout kan worden gecompenseerd door een versterker te gebruiken met een versterking gelijk aan de reciproke van de fout. De twee versterkingen zullen effectief opheffen. Het effect van een offset- en een versterkingsfout wordt getoond in de figuren
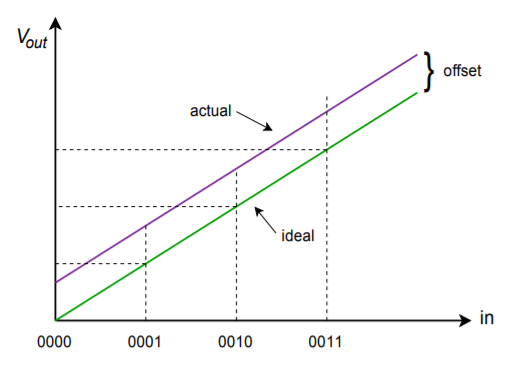
Figuur
(\PageIndex{8}}): Alleen offsetfout.
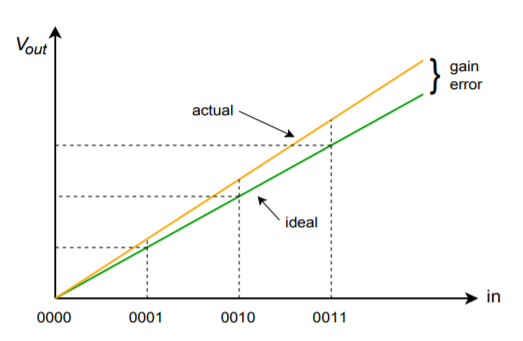
Figuur (\PageIndex{9}}): Alleen versterkingsfout.
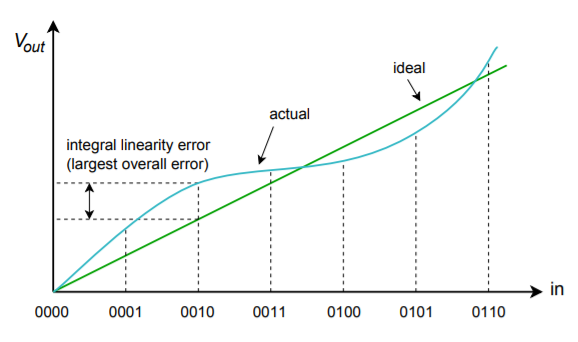
Nonlineariteitsfouten kunnen worden onderverdeeld in twee vormen: integrale niet-lineariteit en differentiële niet-lineariteit. Integrale niet-lineariteit geeft de maximale afwijking aan tussen de ideale en de werkelijke output voor alle mogelijke inputs. Differentiële niet-lineariteit geeft de maximale uitgangsafwijking ten opzichte van één LSB, veroorzaakt door twee aangrenzende ingangswoorden. Als de differentiële niet-lineariteit groter is dan \(\pm1) LSB, kan het systeem niet-monotoon zijn. Met andere woorden, een hoger digitaal ingangswoord kan in feite een lagere analoge uitgangsspanning opleveren. Deze twee vormen van fout worden getoond in figuur \PageIndex{10}\). Merk op dat het mogelijk is om een hoge integrale niet-lineariteit te hebben en toch een bescheiden differentiële niet-lineariteit. Dit is het geval in figuur
Figuur
(\PageIndex{10a}): Lineariteitsfout Integrale lineariteitsfout.
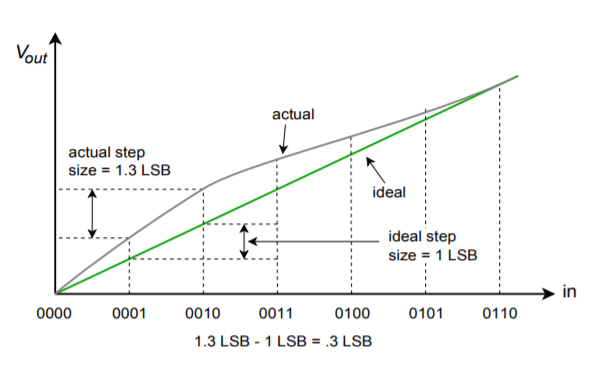
Figuur (\PageIndex{10b}\): Lineariteitsfout (vervolg) Differentiële lineariteitsfout (relatief-naastliggende fout)
Zoals u ziet, is de nauwkeurigheid afhankelijk van tamelijk complexe factoren. In een poging om dit terug te brengen tot een enkel getal, geven sommige fabrikanten een effectief aantal bits specificatie. Bijvoorbeeld, een 16-bit DAC kan worden gespecificeerd als zijnde 14-bit nauwkeurig. Dit betekent dat de 14 meest significante bits zich op de geïdealiseerde manier gedragen, maar dat de laagste 2 bits kunnen worden overstemd door lineariteitsfouten. Een andere specificatie die u soms ziet is “geen ontbrekende codes”. Dit betekent dat voor elke toename van het ingangswoord, er een passende positieve verandering van het uitgangsniveau zal zijn.
In de praktijk wordt de standaard DA-omzetter gebruikt met een uitgangsfilter. Zoals uit de voorgaande figuren blijkt, bevatten de door de DAC geproduceerde golfvormen een trapvormig neveneffect. In het algemeen is dit niet wenselijk. De abrupte veranderingen in het uitgangsniveau geven aan dat er componenten met een hogere frequentie aanwezig zijn. Alle componenten boven de Nyquist frequentie moeten worden weggefilterd met een geschikt laagdoorlaatfilter. Dit filter wordt soms een reconstructie- of afvlakfilter genoemd. In een onjuist ontworpen systeem zal het reconstructiefilter enkele van de hoogste in-band frequentiecomponenten verwijderen (d.w.z. componenten direct onder de Nyquist frequentie). Om dit te compenseren worden logische niveaus vaak gedurende kortere perioden naar de DAC gelatched, waardoor een meer gepiekt uiterlijk ontstaat, in plaats van de trapvorm. Dit effect is te zien in figuur (Pagina-index{11}). Hoewel deze spiked golfvorm minder gewenst lijkt dan de trapvorm, creëert hij hogere niveaus voor de bovenste componenten, en na filtering is het resultaat een vloeiender algemene frequentierespons.
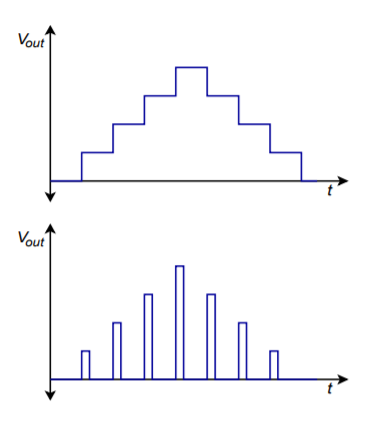
Figuur (\PageIndex{11}\): Reconstructie van de uitgang. a. Volledige periodevergrendeling (boven). b. Gedeeltelijke periodevergrendeling (onder).
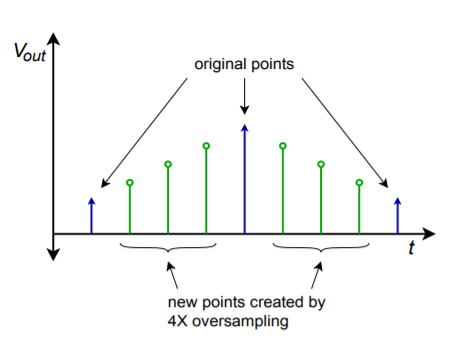
Om de kwaliteit van de uitgangsgolfvorm verder te verbeteren, wordt soms een techniek toegepast die bekend staat als oversampling. Het basisidee is om nieuwe sample-punten te creëren tussen de bestaande. Het resultaat is een veel dichtere datasnelheid, die hopelijk na filtering nauwkeurigere resultaten oplevert. De hogere datasnelheid kan ook de eisen van het reconstructiefilter versoepelen. Een typisch systeem kan viermaal oversampling gebruiken, wat betekent dat de outputdatasnelheid viermaal zo hoog is als het origineel. Daarom moeten voor elk invoerwoord drie nieuwe woorden worden toegevoegd. Dit effect is te zien in figuur
Figuur
(\PageIndex{12}}): Oversampled output.
Er zijn een aantal manieren om de nieuwe sample punten te maken. De meest voor de hand liggende manier is via eenvoudige interpolatie, maar dit levert niet de beste resultaten op. Een andere techniek bestaat erin de nieuwe waarden op nul te initialiseren en vervolgens de gegevensstroom door een digitaal laagdoorlatend filter te voeren, dat in feite de juiste waarden berekent. Een uitbreiding van het oversampling-principe is de delta-sigma-techniek. Bij delta-sigma worden zeer hoge oversampling-snelheden gebruikt in combinatie met gespecialiseerde digitale filteralgoritmen. De algoritmen ruilen in wezen de hogere datasnelheid in voor een langzamere snelheid met een hogere resolutie. Het ontwerp en de analyse van delta-sigma systemen is tamelijk geavanceerd en valt buiten het bestek van deze tekst. Het volstaat te zeggen dat deze technieken de kwaliteit van het uitgangssignaal kunnen verhogen en op grote schaal worden gebruikt in toepassingen zoals audio-CD- en DVD-spelers van hoge kwaliteit.
12.4.2: Digitaal naar analoog converter geïntegreerde schakelingen
Er zijn vele mogelijke toepassingen voor digitaal naar analoog converteerders, en een aantal verschillende chips zijn ontwikkeld om aan specifieke behoeften te voldoen. In het algemeen kunnen deze in specifieke klassen worden ingedeeld, zoals hoge snelheid, hoge resolutie, of lage kostprijs. Wij zullen drie representatieve typen onderzoeken. De apparaten die we zullen bekijken zijn de DAC0832; een basis 8-bit eenheid, de DAC7545; een microprocessor-compatibele 12-bit eenheid, en de PCM1716; een 24-bit hoge-kwaliteit converter die gebruikt wordt in de audio-industrie.
DAC0832
Dit IC is een populaire microprocessor-compatibele 8-bit converter. De DAC0830 en DAC0831 zijn vergelijkbaar, maar met iets mindere prestaties. Het is een vermenigvuldigings-DAC. Met andere woorden, het uitgangssignaal is een functie van het digitale ingangswoord en een referentie-ingang. In sommige toepassingen ligt de referentie-ingang niet vast, maar is het eerder een variabel ingangssignaal. Een overzicht van de kenmerken en de pennenbezetting zijn te zien in figuur (Pagina-Index{13}). Opvallende punten zijn een settling-tijd van slechts 1 s, laag stroomverbruik en hoge lineariteit. De DAC0832 kan zowel in stand-alone modus als met een microprocessor worden gebruikt. De schakelende golfvormen zijn te zien in figuur

Figuur
(\Index{13}): DAC0832. Overgenomen met dank aan Texas Instrutment

Figuurtje (Pagina-index{14}): DAC0832-schakelgolfvormen Overgenomen met dank aan Texas Instrutments
Een interessante toepassing van de DAC0832 is te zien in figuur (PaginaIndex{15}). In principe is dit een digitaal aangestuurd toestandsvariabel filter.
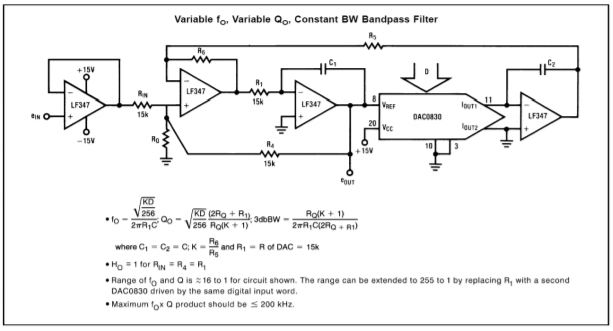
Figuur (\PageIndex{15}\): DAC0832 staats variabel filter toepassing. Overgenomen met dank aan Texas Instrutments
Merk op dat de converter de ingangsweerstand van de tweede integrator vervangt. Normaal zou die weerstand worden gebruikt om de uitgangsspanning van de eerste integrator om te zetten in een ingangsstroom voor de tweede integrator. Deze taak wordt nu uitgevoerd door de DAC0832. Het digitale ingangswoord bepaalt effectief de conversie van spanning naar stroom. Een verandering in het ingangswoord wijzigt dus de afstemfrequentie van het filter, net als een potentiometer. Vergelijk deze schakeling met het spanningsgeregelde OTA-filter uit hoofdstuk 11. Conceptueel lijken ze erg op elkaar.

Figuurtje (Pagina-index{16}): DAC7821. Met dank aan Texas Instruments
DAC7821
De DAC7821 is een vrij standaard 12-bits lineaire converter en is afgebeeld in figuur (\PageIndex{16}\). Interessant is dat het een vermenigvuldigingsconverter is en dat hij compatibel is met een microprocessor. Het vermenigvuldigingseffect is het gevolg van het feit dat een referentie wordt gebruikt om het laddernetwerk (R/2R) aan te sturen. Als de referentie wordt gewijzigd, wordt de uitgang effectief herschaald. U kunt het uitgangssignaal dus zien als gelijk aan de referentiewaarde maal het digitale ingangswoord. U kunt dit ook zien als een vorm van “digitale volumeregeling”.
Met de toevoeging van een paar extra logische lijnen, is het IC microprocessor-compatibel geworden. Dit betekent dat de DAC7821 chip select en lees/schrijf lijnen heeft samen met de 12 data input lijnen. Hierdoor kan de converter rechtstreeks op de microprocessor-databus worden aangesloten. Door gebruik te maken van memory-mapped I/O, kan de microprocessor gegevens naar de converter schrijven net zoals hij gegevens naar het geheugen schrijft. Een 16-bit microprocessorsysteem kan de converter alle benodigde gegevens in één schrijfcyclus voorleggen, maar een 8-bit microprocessor heeft twee schrijfcycli nodig en een of andere vorm van latch. Eén adres kan worden gebruikt voor de onderste 8 bits, en een ander adres voor de resterende 4 bits. Een vereenvoudigd systeem wordt getoond in figuur (Pagina-Index{17}) met een 8-bit microprocessor.
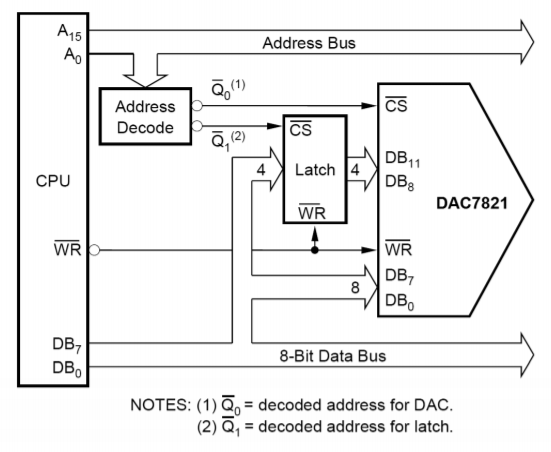
Figuur (Pagina-Index{17}): Interface tussen microprocessor en DAC7821. Met dank aan Texas Instruments
PCM5242
De PCM5242 is een stereo 24-bit converter die speciaal is ontworpen voor digitale audiotoepassingen van hoge kwaliteit. Hij wordt geleverd in een VQFN (Very thin Quad Flat No-lead) pakket. Een blokschema en een lijst met kenmerken zijn te zien in figuur (\PageIndex{18a}). In tegenstelling tot de andere converters, heeft de PCM5242 seriële invoer van gegevens, geen parallelle. De PCM5242 heeft zijn eigen seriële conversiecircuits en logica aan boord. Deze techniek helpt de systeemkosten te drukken. Het is ook verrassend handig omdat veel gespecialiseerde digitale signaalverwerkende IC’s die met de PCM5242 kunnen worden gebruikt, een seriële uitgang hebben. Deze kan rechtstreeks in de PCM5242 worden ingevoerd in 16-, 24-, of 32-bit formaat.

Figuurtje (Pagina-index{18a}): PCM5242. Met dank aan Texas Instruments
Het specificatieblad van de PCM5242 is te zien in figuur (Pagina-index{18b}). Merk op dat dit apparaat is gespecificeerd met bemonsteringsfrequenties van 48 kHz tot 192 kHz. De totale harmonische vervorming plus ruis is typisch 94 dB onder een volle-schaal uitgang bij gebruik met een van deze bemonsteringsfrequenties. Vanwege de hoge resolutie en het dynamisch bereik van 114 dB moet bij het ontwerpen van de schakeling extra aandacht worden besteed aan het voorkomen van brom-pickup en RF-interferentie.
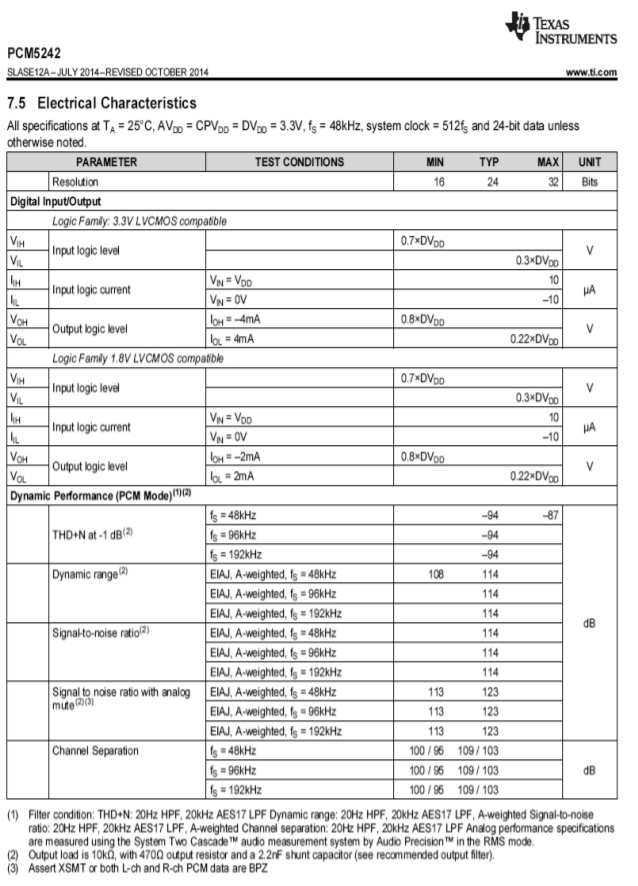
Figuurtje (Pagina-index{18b}): PCM5242 specificaties. Overgenomen met dank aan Texas Instruments
12.4.3: Toepassingen van digitaal-naar-analoog-convertor geïntegreerde schakelingen
Voorbeeld
Het eerste waar veel mensen aan denken als ze de termen digitaal of gedigitaliseerd horen, is misschien wel de audio-cd, of kortweg CD. CD-spelers voor thuisgebruik zijn uitstekende voorbeelden van het gebruik van nauwkeurige DA-schakelingen in ons dagelijks leven. Muziekgegevens worden op de CD opgeslagen met een resolutie van 16 bits en een bemonsteringsfrequentie van 44,1 kHz. Dit levert een Nyquist-frequentie van 22,05 kHz op, wat hoog genoeg is om het gehoorbereik van de meeste mensen te bestrijken. Foutcorrectie en hulpgegevens worden ook op de schijf opgeslagen. De gegevens worden op de schijf opgeslagen in de vorm van zeer kleine putjes, die door een laser worden gelezen. Het signaal wordt vervolgens omgezet in de gebruikelijke elektronische logische vorm, waar het op fouten wordt gecontroleerd en zo nodig aangepast. De datastroom wordt vervolgens aan de DA-omzetter toegevoerd voor de audioreconstructie. Een enkele convertor kan worden gemultiplexed tussen de twee stereokanalen, of er kunnen twee specifieke converters worden gebruikt. Oversampling in het bereik van 2X tot 8X wordt vaak gebruikt voor een betere signaalkwaliteit. Een blokschema van het systeem is afgebeeld in figuur (blz. 19). Het eigenlijke DAC-gedeelte lijkt bijna triviaal in vergelijking met sommige van de meer geavanceerde elementen.
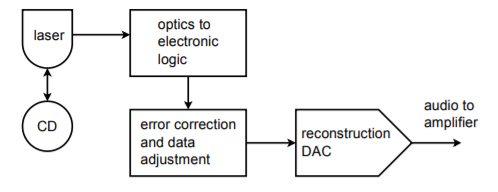
Figuur (PaginaIndex{19}): Afspeelsysteem voor audio-cd’s.
De opslagdichtheid van de optische cd is zeer opmerkelijk. Deze kleine schijf (minder dan 5 inches in diameter) kan 70 minuten muziek bevatten. Als we de hulpgegevens buiten beschouwing laten, kunnen we snel de totale opslagcapaciteit berekenen. We hebben twee kanalen van 16-bit data, of 32 bits (4 bytes) per samplepunt. Er zijn 44.100 samples per seconde gedurende 70 minuten, wat 185,22 megasamples oplevert. De totale data-opslag is 5,927 gigabit, ofwel 741 megabyte.
Voorbeeld(\PageIndex{2})
Zoals reeds gezegd, is het mogelijk DAC’s rechtstreeks op microprocessorsystemen aan te sluiten. Bovendien kan de microprocessor naar de DAC schrijven met niet meer inspanning dan het schrijven naar een geheugenplaats. De microprocessor kan elke gewenste reeks datawoorden naar de DAC schrijven en kan een reeks vrijwel eindeloos herhalen. Met deze mogelijkheid kunnen we een willekeurige golfvormgenerator maken. In plaats van vast te zitten aan een reeks vooraf gedefinieerde golfvormen zoals bij gewone functiegeneratoren, kunnen met dit systeem alle mogelijke golfvormen worden gemaakt. De nauwkeurigheid en flexibiliteit van het systeem zullen afhangen van de snelheid en de beschikbare DAC-resolutie.
Het basisidee is er een van tabel look-up. Laten we bijvoorbeeld zeggen dat we een 16-bits systeem hebben. We maken een tabel met gegevenswaarden voor één cyclus van de uitgangsgolfvorm. Voor het gemak kunnen we de tabelgrootte een handige macht van 2 maken, zoals 256. Met andere woorden, een enkele uitgangscyclus wordt opgedeeld in 256 discrete tijdsblokjes. Het is dus duidelijk dat de omzetter een paar honderd keer sneller moet zijn dan de hoogste grondfrequentie die we willen produceren. Door de uitgangsdatasnelheid te verhogen of te verlagen, kunnen we de frequentie van de uitgangsfundamenten veranderen. Dit staat bekend als een variabele bemonsteringsfrequentietechniek. Het is ook mogelijk de frequentie van de grondtoon te veranderen met een fixed rate techniek (dit is iets ingewikkelder, maar biedt wel bepaalde voordelen). Een stroomdiagram voor de uitvoer is te zien in figuur
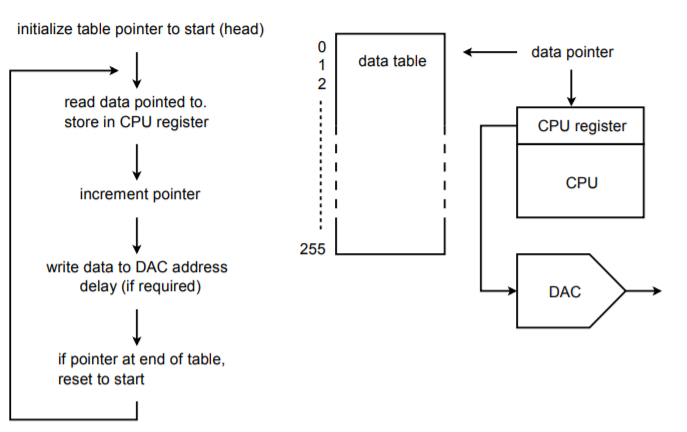
Figuur
(\PageIndex{20}\): Arbitraire golfvormgenerator.
Bij de initialisatie wordt een adrespointer ingesteld op het startadres van de gegevenstabel. De CPU leest de gegevens uit de tabel via de pointer. De pointer wordt opgehoogd, zodat hij nu naar het volgende element in de tabel wijst. (Sommige CPU’s bieden een post-increment adresseringsmodus, zodat beide stappen in een enkele instructie kunnen worden uitgevoerd). Vervolgens schrijft de CPU de gegevens naar het speciale DAC-adres. Op dit punt wordt een of andere software/hardware vertraging in werking gesteld die de uitgangsdatasnelheid instelt. Na de vertraging leest de CPU het volgende data-element via de pointer en gaat verder zoals in de eerste run. Zodra het 256e element is verzonden, wordt de pointer teruggezet naar het begin van de tabel en gaat het proces verder. Op deze manier kan de tabel worden gezien als cirkelvormig, of nooit-eindigend. Indien de systeemsoftware in een taal van een hoger niveau is geschreven, kan de pointer/gegevenstabel worden geïmplementeerd als een eenvoudige array waarbij de array-index wordt ingesteld door een teller. Dit zal echter niet zo efficiënt zijn als een directe aanpak op assemblageniveau.
Het mooie van dit systeem is dat de gegevenstabel vrijwel elke reeks gegevens kan bevatten. De gegevens kunnen een sinus, puls, driehoek of andere standaardfunctie voorstellen. Nog belangrijker is dat de gegevens een sinusgolf met een ruiscomponent of een signaal met een bromcomponent kunnen weergeven. Deze gegevens kunnen van drie basisbronnen afkomstig zijn. Ten eerste kan de gegevenstabel worden gevuld door directe berekeningen indien de tijd-domeinvergelijking van de gewenste functie bekend is. Ten tweede kunnen de gegevens door de gebruiker worden vervaardigd via een of andere vorm van interactie met een computer, misschien met een muis of een tekenblok. Tenslotte kunnen de gegevens worden afgeleid van een signaal uit de werkelijkheid. Dat wil zeggen, een analoog-digitaal-omzetter kan worden gebruikt om het signaal in digitale vorm op te nemen. De gegevens kunnen dan in de tabel worden geladen en herhaaldelijk worden afgespeeld. De arbitrary waveform generator stelt zijn gebruiker in staat schakelingen en systemen te testen met een reeks golfvormen die anders onmogelijk of onpraktisch te genereren zouden zijn.
Voorbeeld (Pagina-Index{3})
Onder computerbesturing kunnen DA-omzetters worden gebruikt als onderdeel van een geautomatiseerd testapparatuursysteem. Om een elektronisch product volledig te karakteriseren, moet een aantal individuele tests worden uitgevoerd. Het opzetten van elke individuele test kan wat tijdrovend zijn en is onderhevig aan bedieningsfouten. Automatisering van deze procedure kan de herhaalbaarheid verbeteren en de testtijd verkorten. Er zijn vele manieren waarop dit proces kan worden geautomatiseerd. We zullen één benadering bekijken.
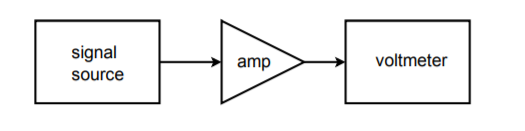
Figuurtje (Pagina-index{21}): Eenvoudige testopstelling.
Laten we eens aannemen dat we frequentieresponsmetingen willen doen voor een versterker bij 20 verschillende frequenties. Een testopstelling voor dit doel is te zien in figuur 21. Om deze test handmatig uit te voeren zijn 20 verschillende instellingen van het bronsignaal nodig, en 20 bijbehorende uitgangsmetingen. Dit kan nogal omslachtig zijn als veel eenheden moeten worden getest. Het zou erg handig zijn als de bronfrequentie op de een of andere manier automatisch kon worden gewijzigd in vooraf ingestelde waarden. Dit is niet bijzonder moeilijk. De meeste moderne bronnen hebben ingangen voor stuurspanning die kunnen worden gebruikt om de frequentie in te stellen. Het vereiste stuurvoltage kan worden gecreëerd en nauwkeurig worden ingesteld met behulp van een computer en een DA-omzetter. De computer kan worden geprogrammeerd om specifieke digitale woorden naar de DAC te sturen, die op zijn beurt de stuuringang van de signaalbron voedt. Met andere woorden, het datawoord bepaalt rechtstreeks de frequentie van de signaalbron. De computer kan worden geprogrammeerd om vrijwel elke opeenvolging van datawoorden met vrijwel elke snelheid te verzenden en dit alles zonder tussenkomst van de operator. Het enige wat de operator hoeft te doen is het proces starten. De herhaalbaarheid van de tests is zeer hoog met een systeem als dit. Een blokschema van dit systeem is te zien in figuur
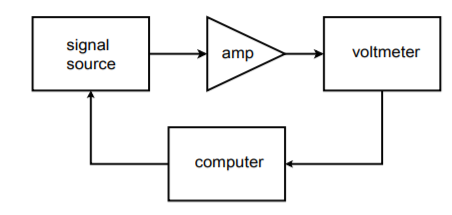
Figuur
(\PageIndex{22}\): Geautomatiseerde testopstelling.
Om de gegevens op te nemen kan de voltmeter worden aangesloten op een stripkaartrecorder, of beter nog, terug naar de computer. De gegevens kunnen in digitale vorm naar de computer worden gezonden als de voltmeter van vrij geavanceerd ontwerp is, of, met de opneming van een analoog-digitaal convertor, kan het outputsignaal direct worden bemonsterd en door de computer worden gemanipuleerd. In beide gevallen kunnen gegevensbestanden worden aangemaakt voor elke geteste eenheid en worden opgeslagen voor later gebruik. Ook kan aan het eind van een testreeks snel een handige statistische analyse worden uitgevoerd. Omdat de DA-omzetter alleen een stuursignaal genereert, is normaal gesproken geen zeer hoge resolutie en lage vervorming vereist. Als een convertor met hoge resolutie wordt gebruikt, is het mogelijk de testsignalen in de computer te maken (zoals in de arbitrary function generator), en af te zien van de signaalbron.
Het geautomatiseerde testsysteem is slechts één mogelijke toepassing van instrumentbesturing. Een ander interessant voorbeeld is het genereren van laser “lichtshows”. Een blokschema van een vereenvoudigd systeem is te zien in figuur (blz. 23). Om de complexe patronen te creëren die het publiek ziet, wordt een laserstraal weerkaatst op kleine bewegende spiegels. De spiegeltjes kunnen gemonteerd zijn op iets simpels als een galvanometer. De galvanometer wordt gevoed door een DAC. Het patroon dat de laserstraal maakt is afhankelijk van de manier waarop de galvanometer de spiegel beweegt, die op zijn beurt wordt gecontroleerd door de datawoorden die aan de DAC worden toegevoerd. In de praktijk kunnen meerdere spiegels worden gebruikt om de straal langs drie assen te laten afbuigen.
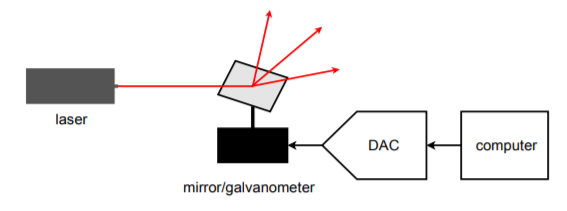
Figuurtje (Pagina-index{23}): Computergestuurde verlichting.
DA-omzetters kunnen worden gebruikt om elk apparaat met een stuurspanningstype ingang te regelen. Zij kunnen ook worden gebruikt om elektromechanische apparaten te regelen die reageren op een toegepaste spanning. Hun echte voordeel is de herhaalbaarheid en flexibiliteit die zij bieden.