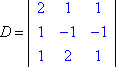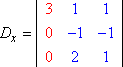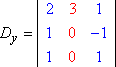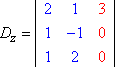De Regel van Cramer

Kom terug naar de lessenindex | Doe de lessen op volgorde | Printvriendelijke pagina

De Regel van Cramer

Gegeven een stelsel lineaire vergelijkingen, is de regel van Cramer een handige manier om slechts één van de variabelen op te lossen zonder het hele stelsel vergelijkingen te hoeven oplossen. Meestal wordt Cramer’s Rule niet op deze manier onderwezen, maar dit zou wel de bedoeling van de regel moeten zijn: in plaats van het hele stelsel op te lossen, kun je Cramer’s gebruiken om op te lossen voor slechts één variabele.

Laten we het volgende stelsel vergelijkingen gebruiken:

2x + y + z = 3
x – y – z = 0
x + 2y + z = 0

We hebben het linkerdeel van het stelsel met de variabelen (de “coëfficiëntenmatrix”) en het rechterdeel met de antwoordwaarden. Zij D de determinant van de coëfficiëntenmatrix van bovenstaand stelsel, en zij Dx de determinant gevormd door de x-kolomwaarden te vervangen door de antwoord-kolomwaarden:

Op dezelfde manier, Dy en Dz zouden dan zijn: Copyright © Elizabeth Stapel 2004-2011 Alle rechten voorbehouden

Evaluatie van elke determinant (met de hier uitgelegde methode), krijgen we:

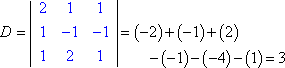
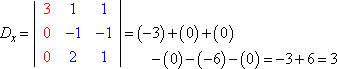
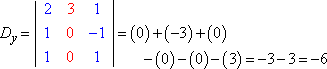
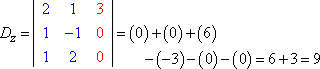
De regel van Kramer zegt dat x = Dx ÷ D, y = Dy ÷ D, en z = Dz ÷ D. Dat is:

x = 3/3 = 1, y = -6/3 = -2, en z = 9/3 = 3

Dat is alles wat de Regel van Cramer inhoudt. Om de variabele te vinden die je wilt (noem het “ß” of “beta”), evalueer je gewoon het determinantquotiënt Dß ÷ D. (Vraag me alsjeblieft niet uit te leggen waarom dit werkt. Vertrouw er maar op dat determinanten vele soorten magie kunnen uitoefenen.)

• Gegeven het volgende stelsel vergelijkingen, vind de waarde van z.

2x + y + z = 1
x – y + 4z = 0
x + 2y – 2z = 3

Om alleen voor z op te lossen, vind ik eerst de determinant van de coëfficiënt.

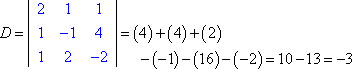
Dan vorm ik Dz door de derde kolom van waarden te vervangen door de antwoordkolom:

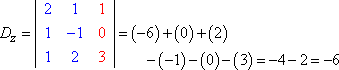
Daarna vorm ik het quotiënt en vereenvoudig:

z = 2

Het punt van de regel van Cramer is dat je niet het hele systeem hoeft op te lossen om die ene waarde te krijgen die je nodig hebt. Dit heeft me veel tijd bespaard bij een aantal natuurkundeproeven. Ik ben vergeten waar we mee bezig waren (iets met draden en stromen, geloof ik), maar de Regel van Cramer was zoveel sneller dan elke andere oplossingsmethode (en God weet dat ik de extra tijd nodig had). Laat je niet in de war brengen door al die subscripts en zo; de Regel is echt heel simpel. Je kiest gewoon de variabele die je wilt oplossen, vervangt de kolom met waarden van die variabele in de coëfficiëntdeterminant door de waarden van de antwoordkolom, evalueert die determinant, en deelt door de coëfficiëntdeterminant. Dat is alles.

Bijna.

Wat als de coëfficiëntdeterminant nul is? Je kunt niet door nul delen, dus wat betekent dat? Ik kan hier niet op de technische details ingaan, maar “D = 0” betekent dat het stelsel van vergelijkingen geen unieke oplossing heeft. Het stelsel kan inconsistent zijn (helemaal geen oplossing) of afhankelijk (een oneindige oplossing, die kan worden uitgedrukt als een parametrische oplossing zoals “(a, a + 3, a – 4)”). In termen van de Regel van Cramer betekent “D = 0” dat je een andere methode moet gebruiken (zoals matrixrijbewerkingen) om het stelsel op te lossen. Als D = 0, kun je de regel van Cramer niet gebruiken.

Top | Terug naar index