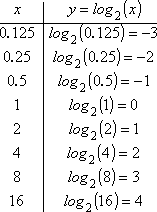Grafiek van logaritmische functies: Inleiding

Terug naar de Lessenindex | Doe de lessen op volgorde | Printvriendelijke pagina

Grafieken van logaritmische functies: Intro (pagina 1 van 3)

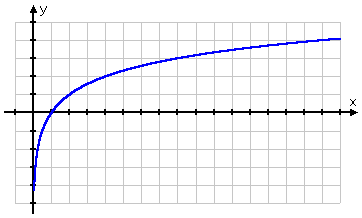
Door de aard van het logaritme hebben de meeste log-grafieken dezelfde vorm, ze lijken op een vierkantswortelgrafiek:

y = sqrt(x)	y = log2(x)

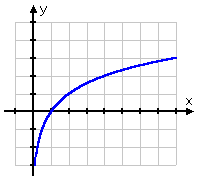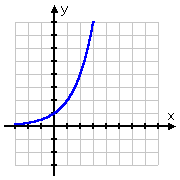
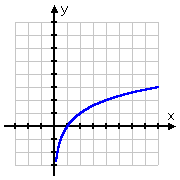
De grafiek van de vierkantswortel begint bij het punt (0, 0) en gaat dan naar rechts. De grafiek van de log daarentegen gaat door (1, 0), gaat naar rechts, maar glijdt ook langs de positieve kant van de y-as naar beneden. Als we bedenken dat logs de inverses van exponentialen zijn, is deze vorm voor de log-grafiek volkomen logisch: de grafiek van de log, die de inverse van de exponentiaal is, zou gewoon de “omkering” van de grafiek van de exponentiaal zijn:

y = 2x	y = log2(x)
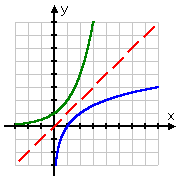
vergelijking van de twee grafieken, aarbij de inversielijn in rood wordt weergegeven

Het is vrij eenvoudig om exponentialen in een grafiek te zetten. Om bijvoorbeeld y = 2x in een grafiek te zetten, voer je een aantal waarden voor x in, berekent de overeenkomstige y-waarden en zet de punten uit. Maar hoe grafiek je logs? Er zijn twee mogelijkheden. Hier is de eerste: Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved

• Grafiek y = log2(x).

Om dit “met de hand” te grafieken, moet ik eerst onthouden dat logs niet gedefinieerd zijn voor negatieve x of voor x = 0. Vanwege deze beperking van het domein (de invoerwaarden) van de log, zal ik niet eens proberen y-waarden te vinden voor bijvoorbeeld x = -3 of x = 0. In plaats daarvan begin ik met x = 1, en werk van daaruit verder, gebruikmakend van de definitie van de log.

Aangezien 20 = 1, dan is log2(1) = 0, en (1, 0) ligt op de grafiek.
Omdat 21 = 2, dan is log2(2) = 1, en (2, 1) ligt op de grafiek.
Omdat 3 geen macht van 2 is, zal log2(3) wel een of andere rommelige waarde zijn. Ik doe dus geen moeite om x = 3 in een grafiek te zetten.
Omdat 22 = 4, dan is log2(4) = 2, en (4, 2) ligt op de grafiek.
Omdat 5, 6, en 7 ook geen machten van 2 zijn, sla ik ze over en ga ik verder met x = 8.
Omdat 23 = 8, dan is log2(8) = 3, dus (8, 3) staat op de grafiek.
De volgende macht van 2 is 16: want 24 = 16, dan is log2(16) = 4, en (16, 4) staat in de grafiek.
De volgende macht van 2, x = 32, is te groot naar mijn smaak; ik heb geen zin om mijn grafiek zo breed te tekenen, dus ik stop bij x = 16.

Het bovenstaande geeft me het punt (1, 0) en enkele punten naar rechts, maar wat doe ik voor x-waarden tussen 0 en 1? Voor dit interval moet ik denken in termen van negatieve machten en reciprocalen. Net zoals de linker “helft” van de exponentiële functie weinig grafiekbare punten had (de rest ligt te dicht bij de x-as), zo heeft ook de onderste “helft” van de logfunctie weinig grafiekbare punten, de rest ligt te dicht bij de y-as. Maar ik kan er wel een paar vinden:

Sinds 2-1 = 1/2 = 0.5, dan log2(0.5) = -1, en (0.5, -1) ligt op de grafiek.

Sinds 2-2 = 1/4 = 0.25, dan log2(0.25) = -2, en (0.25, -2) ligt op de grafiek.

Sinds 2-3 = 1/8 = 0.125, dan log2(0.125) = -3, en (0.125, -3) staat op de grafiek.

De volgende macht van 2 (als x deze kant op gaat) is 1/16 = 2-4, maar de x-waarde voor het punt (0.0625, -4) lijkt me te klein om me er druk over te maken, dus ik zal het maar houden bij de punten die ik al gevonden heb.

Door deze punten op te sommen krijg ik mijn T-diagram:
Teken ik mijn punten en schets ik vervolgens de lijn in (en let op dat ik niet naar links van de y-as ga!), krijg ik deze grafiek:

Top | 1 | 2 | 3 | Terug naar index Volgende >>