Ovaal

Een ovaal is een kromme die lijkt op een geplette cirkel, maar, in tegenstelling tot de ellips, zonder een precieze wiskundige definitie. Het woord ovaal is afgeleid van het Latijnse woord “ovus” voor ei. In tegenstelling tot ellipsen hebben ovalen soms maar één as van spiegelsymmetrie (in plaats van twee).

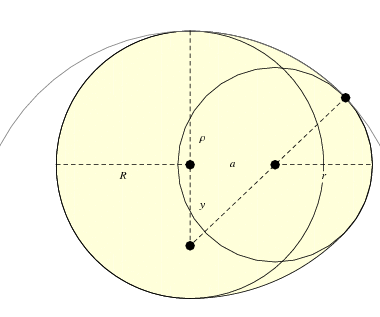
De bijzondere variant die hierboven is afgebeeld kan met een passer worden geconstrueerd door bogen met verschillende stralen zo samen te voegen dat de middelpunten van de bogen op een lijn liggen die door het verbindingspunt gaat (Dixon 1991). Albrecht Dürer gebruikte deze methode om een Romeins lettertype te ontwerpen. Als de scheiding tussen linker- en rechterkap is en de stralen zijn en , respectievelijk, met en , dan is het middelpunt en straal van de verbindingscirkel zijn

			(1)
			(2)

Noem de drie cirkels , en . Zij het bovenste snijpunt van en , zij de hoek tussen de verticale gestippelde lijn en de lijn door , en zij de hoek tussen de horizontale straal van en de stippellijn door . Dan

			(3)
			(4)
			(5)
			(6)

en de helft van de door het ovaal omsloten oppervlakte is de som van de oppervlakten van de meest linkerkwartcirkel, de sector van , en de sector van min de oppervlakte van het driehoekige deel van de sector van dat onder de -as ligt, dus

			(7)
			(8)
			(9)

Zoals verwacht, herleidt deze formule tot de oppervlakte van een cirkel

(10)

voor , en voor de oppervlakte van een stadion

(11)

voor .