Twierdzenia DeMorgana

Matematyk o nazwisku DeMorgan opracował parę ważnych reguł dotyczących dopełniania grup w algebrze Booleana.

Przez dopełnienie grupowe rozumiem dopełnienie grupy wyrażeń, reprezentowane przez długi pasek nad więcej niż jedną zmienną.

Powinniście pamiętać z rozdziału o bramkach logicznych, że odwrócenie wszystkich wejść do bramki odwraca jej zasadniczą funkcję z AND na OR, lub odwrotnie, a także odwraca wyjście.

Tak więc, bramka OR z odwróconymi wszystkimi wejściami (bramka Negative-OR) zachowuje się tak samo jak bramka NAND, a bramka AND z odwróconymi wszystkimi wejściami (bramka Negative-AND) zachowuje się tak samo jak bramka NOR.

Twierdzenia DeMorgana stwierdzają tę samą równoważność w formie „wstecznej”: że odwrócenie wyjścia dowolnej bramki skutkuje taką samą funkcją jak bramka przeciwnego typu (AND vs. OR) z odwróconymi wejściami. OR) z odwróconymi wejściami:

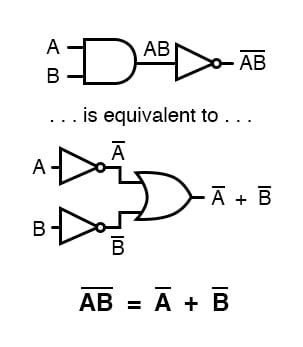
Długi pasek rozciągający się nad pojęciem AB działa jako symbol grupujący i jako taki jest zupełnie inny niż iloczyn A i B niezależnie odwróconych.

Innymi słowy, (AB)' nie jest równe A’B'. Ponieważ symbol „pierwszości” (') nie może być rozciągnięty na dwie zmienne, tak jak pręt, jesteśmy zmuszeni użyć nawiasów, aby zastosować go do całego terminu AB w poprzednim zdaniu.

Abar, jednakże, działa jak własny symbol grupujący, gdy jest rozciągnięty na więcej niż jedną zmienną.

Ma to głęboki wpływ na sposób, w jaki wyrażenia booleańskie są oceniane i redukowane, jak zobaczymy.

Twierdzenie DeMorgana

O twierdzeniu DeMorgana można myśleć w kategoriach łamania symbolu długiego pręta.

Gdy długi pręt jest łamany, operacja bezpośrednio pod łamaniem zmienia się z dodawania na mnożenie, lub odwrotnie, a złamane kawałki pręta pozostają nad poszczególnymi zmiennymi. Dla zilustrowania:

Gdy w wyrażeniu występuje wiele „warstw” prętów, można łamać tylko jeden pręt na raz i na ogół łatwiej jest rozpocząć upraszczanie od łamania najpierw najdłuższego (najwyższego) pręta.

Aby to zilustrować, weźmy wyrażenie (A + (BC)')' i zredukujmy je za pomocą Twierdzenia DeMorgana:

Podążając za radą, by najpierw łamać najdłuższy (najwyższy) pręt, zacznę od łamania pręta obejmującego całe wyrażenie:

W wyniku tego oryginalny układ sprowadza się do trójwejściowej bramki AND z wejściem A odwróconym:

Nigdy nie powinieneś łamać więcej niż jednego pręta w jednym kroku, jak pokazano tutaj:

Jakkolwiek kuszące może być oszczędzanie kroków i łamanie więcej niż jednego pręta na raz, często prowadzi to do błędnego wyniku, więc nie rób tego!

Można poprawnie zredukować to wyrażenie, łamiąc najpierw krótką, a nie długą poprzeczkę:

Efekt końcowy jest taki sam, ale potrzeba więcej kroków w porównaniu z pierwszą metodą, gdzie najpierw łamana jest najdłuższa poprzeczka.

Zauważ, że w trzecim kroku łamiemy długą poprzeczkę w dwóch miejscach.

To jest legalna operacja matematyczna, a nie to samo, co złamanie dwóch prętów w jednym kroku!

Zakaz łamania więcej niż jednego pręta w jednym kroku nie jest zakazem łamania pręta w więcej niż jednym miejscu.

Złamanie w więcej niż jednym miejscu w jednym kroku jest w porządku; złamanie więcej niż jednego pręta w jednym kroku nie jest.

Możesz się zastanawiać, dlaczego nawiasy zostały umieszczone wokół podwyrażenia B' + C', biorąc pod uwagę fakt, że właśnie usunąłem je w następnym kroku.

Zrobiłem to, aby podkreślić ważny, ale łatwo zaniedbywany aspekt twierdzenia DeMorgana.

Ponieważ długi pasek działa jako symbol grupujący, zmienne wcześniej zgrupowane przez złamany pasek muszą pozostać zgrupowane, aby nie utracić właściwego pierwszeństwa (kolejności działania).

W tym przykładzie naprawdę nie miałoby znaczenia, gdybym zapomniał wstawić nawiasy po złamaniu krótkiego paska, ale w innych przypadkach może to mieć znaczenie.

Rozważmy ten przykład, zaczynając od innego wyrażenia:

Jak widać, zachowanie grupowania implikowanego przez paski dopełnienia dla tego wyrażenia jest kluczowe dla uzyskania poprawnej odpowiedzi.

Zastosujmy zasady twierdzenia DeMorgana do uproszczenia obwodu bramkowego:

Jak zawsze, naszym pierwszym krokiem w upraszczaniu tego obwodu musi być wygenerowanie równoważnego wyrażenia boolowskiego.

Możemy to zrobić umieszczając etykietę podwyrażenia na wyjściu każdej bramki, w miarę jak wejścia stają się znane. Oto pierwszy krok w tym procesie:

Następnie możemy oznaczyć wyjścia pierwszej bramki NOR i bramki NAND.

Gdy mamy do czynienia z bramkami o odwróconym wyjściu, łatwiej jest mi napisać wyrażenie dla wyjścia bramki bez końcowej inwersji, ze strzałką wskazującą tuż przed bańką inwersji.

Potem, na przewodzie wychodzącym z bramki (za bańką), piszę pełne, uzupełnione wyrażenie.

W ten sposób mogę się upewnić, że nie zapomniałem o dopełnieniu w podwyrażeniu, ponieważ muszę podzielić zadanie pisania wyrażeń na dwa kroki:

Na koniec piszemy wyrażenie (lub parę wyrażeń) dla ostatniej bramki NOR:

Teraz redukujemy to wyrażenie korzystając z tożsamości, własności, reguł i twierdzeń (DeMorgana) algebry Boole’a:

Obwód bramki równoważnej dla tego znacznie uproszczonego wyrażenia wygląda następująco:

PRZEGLĄD:

• Twierdzenia DeMorgana opisują równoważność między bramkami z odwróconymi wejściami i bramkami z odwróconymi wyjściami. Mówiąc prościej, bramka NAND jest równoważna bramce Negative-OR, a bramka NOR jest równoważna bramce Negative-AND.
• Przy „łamaniu” dopełnienia w wyrażeniu boolowskim, operacja bezpośrednio pod złamaniem (dodawanie lub mnożenie) jest odwracana, a złamane kawałki pozostają nad odpowiednimi wyrażeniami.
• Często łatwiej jest podejść do problemu łamiąc najdłuższy (najwyższy) słupek przed łamaniem słupków pod nim. Nigdy nie wolno próbować łamać dwóch słupków w jednym kroku!
• Słupki uzupełniające funkcjonują jako symbole grupujące. Dlatego, gdy pasek jest łamany, terminy pod nim muszą pozostać zgrupowane. Nawiasy mogą być umieszczone wokół tych zgrupowanych terminów jako pomoc w uniknięciu zmiany pierwszeństwa.

.