Jacobian
br>>
DESCARREGAR Caderno Mathematica
y=f(x) de 
equações em 
variáveis 
, escrito explicitamente como
 |
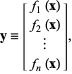(1)
|
ou mais explicitamente como
 |
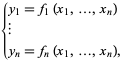(2)
|
a matriz Jacobiana, por vezes simplesmente chamado “o Jacobiano” (Simon e Blume 1994) é definido por
 |
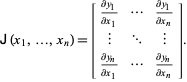(3)
|
O determinante de 
é o determinante Jacobiano (confusamente, frequentemente chamado “o Jacobiano” também) e é denotado
 |
(4)
|
A matriz Jacobiana e determinante pode ser calculado na WolframLanguage usando
JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})
Tomando o diferencial
|
(5)
|
mostra que 
é o determinante da matriz 
, e, portanto, dá as proporções de 
volumes dimensionais (conteúdo) em 
e 
,
 |
(6)
|
Por conseguinte, aparece, por exemplo, no teorema da mudança de variáveis.
O conceito do Jacobiano também pode ser aplicado a 
funções em mais de 
variáveis. Por exemplo, considerando 
e 
, the Jacobians
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
pode ser definido (Kaplan 1984, p. 99).
Para o caso de 
variáveis, o jacobiano toma a forma especial
 |
(9)
|
where 
é o produto ponto e 
é o produto cruzado, que pode ser expandido para dar
 |
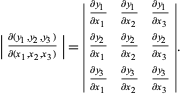(10)
|