Vibration
L’analyse vibratoire (VA), appliquée dans un environnement industriel ou de maintenance vise à réduire les coûts de maintenance et les temps d’arrêt des équipements en détectant les défauts des équipements. VA est une composante clé d’un programme de maintenance conditionnelle (CM), et est souvent appelée maintenance prédictive (PdM). Le plus souvent, VA est utilisé pour détecter les défauts dans les équipements rotatifs (ventilateurs, moteurs, pompes et boîtes de vitesses, etc.) tels que le déséquilibre, le désalignement, les défauts de roulements et les conditions de résonance.
VA peut utiliser les unités de déplacement, de vitesse et d’accélération affichées sous forme de forme d’onde temporelle (TWF), mais le plus souvent, on utilise le spectre, dérivé d’une transformée de Fourier rapide du TWF. Le spectre de vibration fournit des informations importantes sur les fréquences qui permettent de localiser le composant défectueux.
Les principes fondamentaux de l’analyse vibratoire peuvent être compris en étudiant le modèle simple Mass-spring-damper. En effet, même une structure complexe telle que la carrosserie d’une automobile peut être modélisée comme une « sommation » de modèles masse-ressort-amortisseur simples. Le modèle masse-ressort-amortisseur est un exemple d’oscillateur harmonique simple. Les mathématiques utilisées pour décrire son comportement sont identiques à celles d’autres oscillateurs harmoniques simples tels que le circuit RLC.
Note : Cet article ne comprend pas les dérivations mathématiques étape par étape, mais se concentre sur les principales équations et concepts de l’analyse des vibrations. Veuillez vous référer aux références à la fin de l’article pour les dérivations détaillées.
Vibration libre sans amortissementModification

.
Pour commencer l’étude de la masse-ressort-amortisseur, supposons que l’amortissement est négligeable et qu’il n’y a pas de force extérieure appliquée à la masse (i.c’est-à-dire une vibration libre). La force appliquée à la masse par le ressort est proportionnelle à l’étirement « x » du ressort (en supposant que le ressort est déjà comprimé en raison du poids de la masse). La constante de proportionnalité, k, est la rigidité du ressort et a pour unité la force/distance (par exemple lbf/in ou N/m). Le signe négatif indique que la force s’oppose toujours au mouvement de la masse qui lui est attachée :
F s = – k x . {\displaystyle F_{s}=-kx.\!}

La force générée par la masse est proportionnelle à l’accélération de la masse comme le donne la deuxième loi du mouvement de Newton:
Σ F = m a = m x ¨ = m d 2 x d t 2 . {\displaystyle \Sigma \NF=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}.}

La somme des forces sur la masse génère alors cette équation différentielle ordinaire : m x ¨ + k x = 0. {\displaystyle \{\ddot {x}}+kx=0.}


En supposant que l’initiation de la vibration commence par l’étirement du ressort de la distance de A et le relâchement, la solution de l’équation ci-dessus qui décrit le mouvement de la masse est :
x ( t ) = A cos ( 2 π f n t ) . {\displaystyle x(t)=A\cos(2\pi f_{n}t).\!}

Cette solution dit qu’il oscillera avec un mouvement harmonique simple qui a une amplitude de A et une fréquence de fn. Le nombre fn est appelé la fréquence naturelle non amortie. Pour le système masse-ressort simple, fn est défini comme:
f n = 1 2 π k m . {\displaystyle f_{n}={1 \over {2\pi }}{\sqrt {k \over m}}.\!}

Note : la fréquence angulaire ω (ω=2 π f) avec les unités de radians par seconde est souvent utilisée dans les équations car elle simplifie les équations, mais elle est normalement convertie en fréquence ordinaire (unités de Hz ou de manière équivalente cycles par seconde) lorsqu’on énonce la fréquence d’un système. Si la masse et la rigidité du système sont connues, la formule ci-dessus permet de déterminer la fréquence à laquelle le système vibre une fois mis en mouvement par une perturbation initiale. Tout système vibrant possède une ou plusieurs fréquences naturelles auxquelles il vibre une fois perturbé. Cette relation simple peut être utilisée pour comprendre en général ce qui arrive à un système plus complexe une fois que nous ajoutons de la masse ou de la rigidité. Par exemple, la formule ci-dessus explique pourquoi, lorsqu’une voiture ou un camion est entièrement chargé, la suspension se sent ″softer″ que sans charge – la masse a augmenté, réduisant la fréquence naturelle du système.
Ce qui fait vibrer le système : du point de vue de la conservation de l’énergieEdit
Le mouvement vibratoire pourrait être compris en termes de conservation de l’énergie. Dans l’exemple ci-dessus, le ressort a été allongé d’une valeur de x et donc une certaine énergie potentielle ( 1 2 k x 2 {\displaystyle {\tfrac {1}{2}}kx^{2}}).

) est stockée dans le ressort. Une fois relâché, le ressort tend à revenir à son état non étiré (qui est l’état d’énergie potentielle minimale) et, ce faisant, accélère la masse. Au point où le ressort a atteint son état non étiré, toute l’énergie potentielle que nous avons fournie en l’étirant a été transformée en énergie cinétique ( 1 2 m v 2 {\displaystyle {\tfrac {1}{2}}mv^{2}}}.

). La masse commence alors à décélérer car elle comprime maintenant le ressort et, ce faisant, retransmet l’énergie cinétique à son potentiel. Ainsi, l’oscillation du ressort équivaut au transfert aller-retour de l’énergie cinétique en énergie potentielle. Dans ce modèle simple, la masse continue à osciller éternellement à la même magnitude – mais dans un système réel, l’amortissement dissipe toujours l’énergie, ce qui finit par amener le ressort au repos.
Vibration libre avec amortissementModification

Lorsqu’un amortisseur « visqueux » est ajouté au modèle, celui-ci produit une force proportionnelle à la vitesse de la masse. L’amortissement est dit visqueux car il modélise les effets d’un fluide à l’intérieur d’un objet. La constante de proportionnalité c est appelée le coefficient d’amortissement et a pour unité la Force sur la vitesse (lbf⋅s/in ou N⋅s/m).
F d = – c v = – c x ˙ = – c d x d t . {\displaystyle F_{\text{d}}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}.}

La somme des forces sur la masse donne l’équation différentielle ordinaire suivante:
m x ¨ + c x ˙ + k x = 0. {\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0.}

La solution de cette équation dépend de la quantité d’amortissement. Si l’amortissement est suffisamment faible, le système vibre toujours – mais finit, avec le temps, par ne plus vibrer. Ce cas est appelé sous-amortissement, ce qui est important dans l’analyse des vibrations. Si l’amortissement est augmenté juste au point où le système n’oscille plus, le système a atteint le point d’amortissement critique. Si l’amortissement est augmenté au-delà de l’amortissement critique, le système est suramorcé. La valeur que doit atteindre le coefficient d’amortissement pour un amortissement critique dans le modèle masse-ressort-amortisseur est :
c c = 2 km . {\displaystyle c_{\text{c}}=2{\sqrt {\text{km}}.}

Pour caractériser la quantité d’amortissement dans un système, on utilise un rapport appelé rapport d’amortissement (également appelé facteur d’amortissement et % d’amortissement critique). Ce rapport d’amortissement est juste un rapport entre l’amortissement réel et la quantité d’amortissement nécessaire pour atteindre l’amortissement critique. La formule du rapport d’amortissement ( ζ {\displaystyle \zeta }

) du modèle masse-ressort-amortisseur est : ζ = c 2 km . {\displaystyle \zeta ={c \over 2{\sqrt {\text{km}}}}.}

Par exemple, les structures métalliques (fuselages d’avions, vilebrequins de moteurs) ont des facteurs d’amortissement inférieurs à 0,05, tandis que les suspensions automobiles sont de l’ordre de 0,2-0,3. La solution du système sous-amorti pour le modèle masse-ressort-amortisseur est la suivante :
x ( t ) = X e – ζ ω n t cos ( 1 – ζ 2 ω n t – ϕ ) , ω n = 2 π f n . {\displaystyle x(t)=Xe^{-\zeta \omega _{n}t}\cos \left({\sqrt {1-\zeta ^{2}}\omega _{n}t-\phi \right),\qquad \omega _{n}=2\pi f_{n}.}


La valeur de X, la magnitude initiale, et ϕ , {\displaystyle \phi ,}

le déphasage, sont déterminés par la quantité d’étirement du ressort. Les formules pour ces valeurs peuvent être trouvées dans les références.
Fréquences propres amorties et non amortiesModification
Les principaux points à noter de la solution sont le terme exponentiel et la fonction cosinus. Le terme exponentiel définit la vitesse à laquelle le système » s’amortit » – plus le rapport d’amortissement est grand, plus il s’amortit rapidement jusqu’à zéro. La fonction cosinus est la partie oscillante de la solution, mais la fréquence des oscillations est différente de celle du cas non amorti.
La fréquence dans ce cas est appelée « fréquence naturelle amortie », f d , {\displaystyle f_{\text{d}},}

et est liée à la fréquence naturelle non amortie par la formule suivante : f d = f n 1 – ζ 2 . {\displaystyle f_{\text{d}}=f_{n}{\sqrt {1-\zeta ^{2}}.}

La fréquence propre amortie est inférieure à la fréquence propre non amortie, mais pour de nombreux cas pratiques, le rapport d’amortissement est relativement faible et donc la différence est négligeable. Par conséquent, la description amortie et non amortie est souvent abandonnée lors de l’énoncé de la fréquence naturelle (par exemple, avec un rapport d’amortissement de 0,1, la fréquence naturelle amortie n’est inférieure que de 1% à celle non amortie).
Les graphiques sur le côté présentent comment les rapports d’amortissement de 0,1 et 0,3 affectent la façon dont le système » sonne » au fil du temps. Ce qui est souvent fait dans la pratique est de mesurer expérimentalement la vibration libre après un impact (par exemple par un marteau), puis de déterminer la fréquence naturelle du système en mesurant le taux d’oscillation, ainsi que le rapport d’amortissement en mesurant le taux de décroissance. La fréquence naturelle et le rapport d’amortissement ne sont pas seulement importants en vibration libre, mais caractérisent également le comportement d’un système en vibration forcée.
Vibration forcée avec amortissementEdit
Le comportement du modèle de masse-ressort-amortisseur varie avec l’ajout d’une force harmonique. Une force de ce type peut, par exemple, être générée par un déséquilibre rotatif.
F = F 0 sin ( 2 π f t ) . {\displaystyle F=F_{0}\sin(2\pi ft).\!}

La somme des forces sur la masse donne l’équation différentielle ordinaire suivante:
m x ¨ + c x ˙ + k x = F 0 sin ( 2 π f t ) . {\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F_{0}\sin(2\pi ft).}

La solution en régime permanent de ce problème peut être écrite comme:
x ( t ) = X sin ( 2 π f t + ϕ ) . {\displaystyle x(t)=X\sin(2\pi ft+\phi ).\!}

Le résultat indique que la masse oscillera à la même fréquence, f, de la force appliquée, mais avec un déphasage ϕ . isplaystyle \phi .}

L’amplitude de la vibration « X » est définie par la formule suivante.
X = F 0 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 . {\displaystyle X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}.}

Où « r » est défini comme le rapport de la fréquence de la force harmonique sur la fréquence naturelle non amortie du modèle masse-ressort-amortisseur.
r = f f n . {\displaystyle r={\frac {f}{f_{n}}.}

Le déphasage, ϕ , {\displaystyle \phi ,}

est défini par la formule suivante . ϕ = arctan ( – 2 ζ r 1 – r 2 ) . {\displaystyle \phi =\arctan \left({\frac {-2\zeta r}{1-r^{2}}\right).}


Le tracé de ces fonctions, appelé « réponse fréquentielle du système », présente l’une des caractéristiques les plus importantes des vibrations forcées. Dans un système légèrement amorti, lorsque la fréquence de forçage s’approche de la fréquence naturelle ( r ≈ 1 {\displaystyle r\approx 1}

), l’amplitude de la vibration peut devenir extrêmement élevée. Ce phénomène est appelé résonance (par la suite, la fréquence naturelle d’un système est souvent appelée fréquence de résonance). Dans les systèmes de paliers de rotor, toute vitesse de rotation qui excite une fréquence de résonance est appelée vitesse critique.
Si une résonance se produit dans un système mécanique, elle peut être très nuisible – conduisant à une défaillance éventuelle du système. Par conséquent, l’une des principales raisons de l’analyse vibratoire est de prévoir quand ce type de résonance peut se produire, puis de déterminer les mesures à prendre pour l’empêcher de se produire. Comme le montre le tracé de l’amplitude, l’ajout d’un amortissement peut réduire considérablement l’ampleur de la vibration. L’amplitude peut également être réduite si la fréquence naturelle peut être éloignée de la fréquence de forçage en modifiant la rigidité ou la masse du système. Si le système ne peut pas être changé, peut-être que la fréquence de forçage peut être décalée (par exemple, en changeant la vitesse de la machine générant la force).
Voici quelques autres points concernant la vibration forcée montrée dans les graphiques de réponse en fréquence.
- À un rapport de fréquence donné, l’amplitude de la vibration, X, est directement proportionnelle à l’amplitude de la force F 0 {\displaystyle F_{0}}.
(par ex. si on double la force, la vibration double)
- Avec peu ou pas d’amortissement, la vibration est en phase avec la fréquence de forçage lorsque le rapport de fréquence r < 1 et déphasée de 180 degrés lorsque le rapport de fréquence r > 1
- Lorsque r ≪ 1, l’amplitude est juste la déviation du ressort sous la force statique F 0 . {\displaystyle F_{0}.}
Cette déviation est appelée la déviation statique δ s t . {\displaystyle \delta _{st}.}
Par conséquent, lorsque r ≪ 1, les effets de l’amortisseur et de la masse sont minimes.
- Lorsque r ≫ 1, l’amplitude de la vibration est en fait inférieure à la déviation statique δ s t . {\displaystyle \delta _{st}.}
Dans cette région, la force générée par la masse (F = ma) est dominante car l’accélération vue par la masse augmente avec la fréquence. Comme la déviation vue dans le ressort, X, est réduite dans cette région, la force transmise par le ressort (F = kx) à la base est réduite. Par conséquent, le système masse-ressort-amortisseur isole la force harmonique de la base de montage – ce que l’on appelle l’isolation des vibrations. Un amortissement plus important réduit en fait les effets de l’isolation des vibrations lorsque r ≫ 1 car la force d’amortissement (F = cv) est également transmise à la base.
- quel que soit l’amortissement, la vibration est déphasée de 90 degrés par rapport à la fréquence de forçage lorsque le rapport de fréquence r = 1, ce qui est très utile lorsqu’il s’agit de déterminer la fréquence naturelle du système.
- Quel que soit l’amortissement, lorsque r ≫ 1, la vibration est déphasée de 180 degrés par rapport à la fréquence de forçage
- Quel que soit l’amortissement, lorsque r ≪ 1, la vibration est en phase avec la fréquence de forçage
Causes de résonanceEdit
La résonance est simple à comprendre si le ressort et la masse sont considérés comme des éléments de stockage d’énergie – la masse stockant l’énergie cinétique et le ressort stockant l’énergie potentielle. Comme nous l’avons vu précédemment, lorsque la masse et le ressort ne sont soumis à aucune force extérieure, ils transfèrent l’énergie dans les deux sens à un taux égal à la fréquence naturelle. En d’autres termes, pour pomper efficacement l’énergie dans la masse et le ressort, il faut que la source d’énergie alimente l’énergie à un taux égal à la fréquence naturelle. Appliquer une force à la masse et au ressort est similaire à pousser un enfant sur une balançoire, une poussée est nécessaire au bon moment pour que la balançoire monte de plus en plus haut. Comme dans le cas de la balançoire, la force appliquée n’a pas besoin d’être élevée pour obtenir de grands mouvements, mais doit juste ajouter de l’énergie au système.
L’amortisseur, au lieu de stocker de l’énergie, dissipe de l’énergie. Comme la force d’amortissement est proportionnelle à la vitesse, plus le mouvement est important, plus l’amortisseur dissipe l’énergie. Par conséquent, il existe un point où l’énergie dissipée par l’amortisseur est égale à l’énergie ajoutée par la force. À ce moment-là, le système a atteint son amplitude maximale et continuera à vibrer à ce niveau tant que la force appliquée restera la même. S’il n’y a pas d’amortissement, il n’y a rien pour dissiper l’énergie et, théoriquement, le mouvement continuera à croître à l’infini.
Application de forces « complexes » au modèle masse-ressort-amortisseurModification
Dans une section précédente, seule une force harmonique simple a été appliquée au modèle, mais cela peut être étendu considérablement en utilisant deux outils mathématiques puissants. Le premier est la transformée de Fourier qui prend un signal en fonction du temps (domaine temporel) et le décompose en ses composantes harmoniques en fonction de la fréquence (domaine fréquentiel). Par exemple, en appliquant une force au modèle masse-ressort-amortisseur qui répète le cycle suivant : une force égale à 1 newton pendant 0,5 seconde, puis aucune force pendant 0,5 seconde. Ce type de force a la forme d’une onde carrée de 1 Hz.
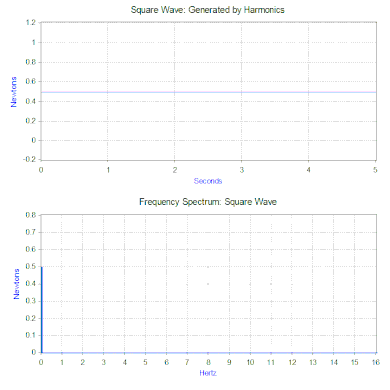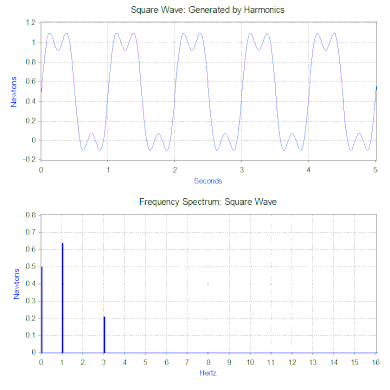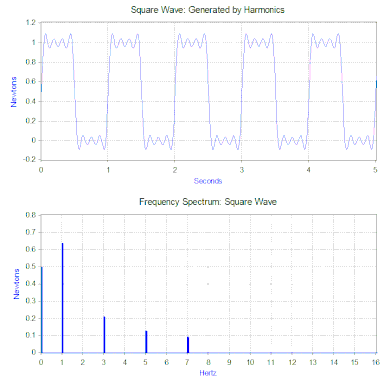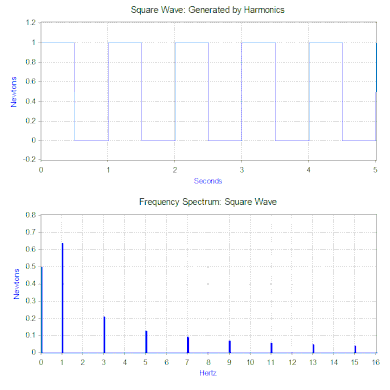
La transformée de Fourier de l’onde carrée génère un spectre de fréquence qui présente l’amplitude des harmoniques qui composent l’onde carrée (la phase est également générée, mais elle est généralement moins préoccupante et n’est donc souvent pas tracée). La transformée de Fourier peut également être utilisée pour analyser des fonctions non périodiques telles que des transitoires (par exemple, des impulsions) et des fonctions aléatoires. La transformée de Fourier est presque toujours calculée en utilisant l’algorithme informatique de la transformée de Fourier rapide (FFT) en combinaison avec une fonction de fenêtre.
Dans le cas de notre force à onde carrée, la première composante est en fait une force constante de 0,5 newton et est représentée par une valeur à 0 Hz dans le spectre de fréquence. La composante suivante est une onde sinusoïdale de 1 Hz dont l’amplitude est de 0,64. Elle est représentée par la ligne à 1 Hz. Les autres composantes sont à des fréquences impaires et il faut une quantité infinie d’ondes sinusoïdales pour générer l’onde carrée parfaite. Par conséquent, la transformée de Fourier permet d’interpréter la force comme une somme de forces sinusoïdales appliquées au lieu d’une force plus » complexe » (par exemple une onde carrée).
Dans la section précédente, la solution de vibration a été donnée pour une seule force harmonique, mais la transformée de Fourier donne en général des forces harmoniques multiples. Le deuxième outil mathématique, « le principe de superposition », permet de sommer les solutions de plusieurs forces si le système est linéaire. Dans le cas du modèle ressort-masse-amortisseur, le système est linéaire si la force du ressort est proportionnelle au déplacement et l’amortissement est proportionnel à la vitesse sur la plage de mouvement concernée. Par conséquent, la solution au problème avec une onde carrée consiste à additionner la vibration prédite de chacune des forces harmoniques trouvées dans le spectre de fréquence de l’onde carrée.
Modèle de réponse en fréquenceÉdition
La solution d’un problème de vibration peut être considérée comme une relation entrée/sortie – où la force est l’entrée et la sortie est la vibration. La représentation de la force et de la vibration dans le domaine fréquentiel (magnitude et phase) permet d’obtenir la relation suivante :
X ( i ω ) = H ( i ω ) ⋅ F ( i ω ) ou H ( i ω ) = X ( i ω ) F ( i ω ) . {\displaystyle X(i\omega )=H(i\omega )\cdot F(i\omega ){\text{ or }}H(i\omega )={X(i\omega )\over F(i\omega )}.}

H ( i ω ) {\displaystyle H(i\omega )}

est appelée fonction de réponse en fréquence (également appelée fonction de transfert, mais pas aussi précise techniquement) et possède à la fois une composante d’amplitude et de phase (si elle est représentée sous forme de nombre complexe, une composante réelle et imaginaire). La magnitude de la fonction de réponse en fréquence (FRF) a été présentée précédemment pour le système masse-ressort-amortisseur. | H ( i ω ) | = | X ( i ω ) F ( i ω ) | = 1 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 , où r = f f n = ω ω n . {\displaystyle |H(i\omega )|=\left|{X(i\omega ) \over F(i\omega )}right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},{\text{ où }}r={\frac {f}{f_{n}}={\frac {\omega }{\i}omega _{n}}.}

La phase de la FRF a également été présentée précédemment comme:
∠ H ( i ω ) = – arctan ( 2 ζ r 1 – r 2 ) . {\displaystyle \angle H(i\omega )=-\arctan \left({\frac {2\zeta r}{1-r^{2}}}\right).}


Par exemple, le calcul de la FRF pour un système masse-ressort-amortisseur avec une masse de 1 kg, une raideur du ressort de 1.93 N/mm et un rapport d’amortissement de 0,1. Les valeurs du ressort et de la masse donnent une fréquence naturelle de 7 Hz pour ce système spécifique. L’application de l’onde carrée de 1 Hz obtenue précédemment permet de calculer la vibration prévue de la masse. La figure illustre la vibration résultante. Il se trouve que dans cet exemple, la quatrième harmonique de l’onde carrée tombe à 7 Hz. La réponse en fréquence de l’amortisseur masse-ressort produit donc une vibration élevée de 7 Hz, même si la force d’entrée avait une harmonique relativement faible de 7 Hz. Cet exemple souligne que la vibration résultante dépend à la fois de la fonction de forçage et du système auquel la force est appliquée.
La figure montre également la représentation dans le domaine temporel de la vibration résultante. Ceci est réalisé en effectuant une transformation de Fourier inverse qui convertit les données du domaine fréquentiel en domaine temporel. En pratique, cela est rarement fait car le spectre de fréquence fournit toutes les informations nécessaires.
La fonction de réponse en fréquence (FRF) ne doit pas nécessairement être calculée à partir de la connaissance de la masse, de l’amortissement et de la rigidité du système – mais elle peut être mesurée expérimentalement. Par exemple, si une force connue sur une gamme de fréquences est appliquée, et si les vibrations associées sont mesurées, la fonction de réponse en fréquence peut être calculée, caractérisant ainsi le système. Cette technique est utilisée dans le domaine de l’analyse modale expérimentale pour déterminer les caractéristiques de vibration d’une structure.


