Vibration
Die Schwingungsanalyse (VA), die in einer Industrie- oder Wartungsumgebung angewendet wird, zielt darauf ab, die Wartungskosten und die Ausfallzeiten von Anlagen durch die Erkennung von Anlagenfehlern zu reduzieren. VA ist eine Schlüsselkomponente eines Zustandsüberwachungsprogramms (CM) und wird oft als vorausschauende Wartung (PdM) bezeichnet. Am häufigsten wird VA zur Erkennung von Fehlern in rotierenden Anlagen (Ventilatoren, Motoren, Pumpen, Getriebe usw.) eingesetzt, wie z. B. Unwucht, Ausrichtungsfehler, Wälzlagerfehler und Resonanzbedingungen.
VA kann die Einheiten Weg, Geschwindigkeit und Beschleunigung verwenden, die als Zeitsignal (TWF) angezeigt werden, aber am häufigsten wird das Spektrum verwendet, das aus einer schnellen Fourier-Transformation der TWF abgeleitet wird. Das Schwingungsspektrum liefert wichtige Frequenzinformationen, mit denen die fehlerhafte Komponente lokalisiert werden kann.
Die Grundlagen der Schwingungsanalyse lassen sich anhand des einfachen Masse-Feder-Dämpfer-Modells verstehen. In der Tat kann sogar eine komplexe Struktur wie eine Autokarosserie als eine „Summierung“ von einfachen Masse-Feder-Dämpfer-Modellen modelliert werden. Das Masse-Feder-Dämpfer-Modell ist ein Beispiel für einen einfachen harmonischen Oszillator. Die Mathematik, die zur Beschreibung seines Verhaltens verwendet wird, ist identisch mit anderen einfachen harmonischen Oszillatoren, wie z. B. der RLC-Schaltung.
Hinweis: Dieser Artikel enthält nicht die schrittweisen mathematischen Ableitungen, sondern konzentriert sich auf die wichtigsten Gleichungen und Konzepte der Schwingungsanalyse. Bitte beachten Sie die Referenzen am Ende des Artikels für detaillierte Ableitungen.
Freies Schwingen ohne DämpfungBearbeiten

Zu Beginn der Untersuchung des Masse-Feder-Dämpfers wird angenommen, dass die Dämpfung vernachlässigbar ist und dass keine äußere Kraft auf die Masse wirkt (d. h.d. h. freie Schwingung). Die Kraft, die von der Feder auf die Masse ausgeübt wird, ist proportional zu dem Betrag, um den die Feder „x“ gedehnt wird (unter der Annahme, dass die Feder bereits durch das Gewicht der Masse zusammengedrückt ist). Die Proportionalitätskonstante k ist die Steifigkeit der Feder und hat die Einheit Kraft/Weg (z.B. lbf/in oder N/m). Das negative Vorzeichen zeigt an, dass die Kraft immer der Bewegung der an ihr befestigten Masse entgegenwirkt:
F s = – k x . {\displaystyle F_{s}=-kx.\!}

Die von der Masse erzeugte Kraft ist proportional zur Beschleunigung der Masse, wie durch das zweite Newtonsche Bewegungsgesetz gegeben:
Σ F = m a = m x ¨ = m d 2 x d t 2 . {\displaystyle \Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}.}

Die Summe der Kräfte auf die Masse ergibt dann diese gewöhnliche Differentialgleichung: m x ¨ + k x = 0. {\displaystyle \ m{\ddot {x}}+kx=0.}


Angenommen, die Einleitung der Schwingung beginnt, indem die Feder um die Strecke A gedehnt und losgelassen wird, lautet die Lösung der obigen Gleichung, die die Bewegung der Masse beschreibt:
x ( t ) = A cos ( 2 π f n t ) .
displaystyle x(t)=A cos(2 π f_{n}t).

Diese Lösung besagt, dass es mit einer einfachen harmonischen Bewegung schwingen wird, die eine Amplitude von A und eine Frequenz von fn hat. Die Zahl fn wird die ungedämpfte Eigenfrequenz genannt. Für das einfache Masse-Feder-System ist fn definiert als:
f n = 1 2 π k m . {\displaystyle f_{n}={1 \über {2\pi }}{\sqrt {k \über m}}.\!}

Hinweis: Die Winkelfrequenz ω (ω=2 π f) mit den Einheiten Bogenmaß pro Sekunde wird oft in Gleichungen verwendet, weil sie die Gleichungen vereinfacht, wird aber normalerweise in die gewöhnliche Frequenz (Einheiten Hz oder äquivalent Zyklen pro Sekunde) umgewandelt, wenn die Frequenz eines Systems angegeben wird. Wenn die Masse und Steifigkeit des Systems bekannt sind, kann mit der obigen Formel die Frequenz bestimmt werden, mit der das System schwingt, sobald es durch eine anfängliche Störung in Bewegung gesetzt wird. Jedes schwingende System hat eine oder mehrere Eigenfrequenzen, bei denen es schwingt, sobald es gestört wird. Diese einfache Beziehung kann verwendet werden, um allgemein zu verstehen, was mit einem komplexeren System passiert, sobald wir Masse oder Steifigkeit hinzufügen. Die obige Formel erklärt zum Beispiel, warum sich die Federung eines voll beladenen Autos oder Lastwagens ″weicher″ anfühlt als im unbeladenen Zustand – die Masse hat sich erhöht, wodurch die Eigenfrequenz des Systems sinkt.
Was das System zum Schwingen bringt: aus Sicht der Energieerhaltung
Schwingungsbewegungen können im Sinne der Energieerhaltung verstanden werden. Im obigen Beispiel ist die Feder um einen Wert von x gedehnt worden und damit eine gewisse potentielle Energie ( 1 2 k x 2 {\displaystyle {\tfrac {1}{2}}kx^{2}}

) in der Feder gespeichert ist. Nach dem Loslassen neigt die Feder dazu, in ihren ungedehnten Zustand zurückzukehren (das ist der Zustand minimaler potentieller Energie) und beschleunigt dabei die Masse. An dem Punkt, an dem die Feder ihren ungedehnten Zustand erreicht hat, ist die gesamte potentielle Energie, die wir durch das Dehnen der Feder zugeführt haben, in kinetische Energie umgewandelt worden ( 1 2 m v 2 {\displaystyle {\tfrac {1}{2}}mv^{2}}

). Die Masse beginnt dann abzubremsen, weil sie nun die Feder zusammendrückt und dabei die kinetische Energie wieder in ihr Potential überführt. Die Schwingung der Feder läuft also auf ein Hin- und Herübertragen der kinetischen Energie in potentielle Energie hinaus. In diesem einfachen Modell schwingt die Masse ewig mit der gleichen Größe weiter – aber in einem realen System führt die Dämpfung die Energie immer ab und bringt die Feder schließlich zur Ruhe.
Freies Schwingen mit DämpfungBearbeiten

Wenn dem Modell ein „viskoser“ Dämpfer hinzugefügt wird, gibt dieser eine Kraft ab, die proportional zur Geschwindigkeit der Masse ist. Die Dämpfung wird als viskos bezeichnet, weil sie die Auswirkungen einer Flüssigkeit innerhalb eines Objekts modelliert. Die Proportionalitätskonstante c wird als Dämpfungskoeffizient bezeichnet und hat die Einheit Kraft über Geschwindigkeit (lbf⋅s/in oder N⋅s/m).
F d = – c v = – c x ˙ = – c d x d t . {\displaystyle F_{\text{d}}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}.}

Die Summierung der Kräfte auf die Masse ergibt die folgende gewöhnliche Differentialgleichung:
m x ¨ + c x ˙ + k x = 0. {\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0.}

Die Lösung dieser Gleichung hängt von der Höhe der Dämpfung ab. Wenn die Dämpfung klein genug ist, schwingt das System immer noch – aber mit der Zeit hört es auf zu schwingen. Dieser Fall wird als Unterdämpfung bezeichnet, die in der Schwingungsanalyse wichtig ist. Wenn die Dämpfung nur bis zu dem Punkt erhöht wird, an dem das System nicht mehr schwingt, hat das System den Punkt der kritischen Dämpfung erreicht. Wenn die Dämpfung über die kritische Dämpfung hinaus erhöht wird, ist das System überdämpft. Der Wert, den der Dämpfungskoeffizient für eine kritische Dämpfung im Masse-Feder-Dämpfer-Modell erreichen muss, ist:
c c = 2 km . {\displaystyle c_{\text{c}}=2{\sqrt {\text{km}}}.}

Um das Ausmaß der Dämpfung in einem System zu charakterisieren, wird ein Verhältnis verwendet, das Dämpfungsverhältnis (auch bekannt als Dämpfungsfaktor und % kritische Dämpfung). Dieses Dämpfungsverhältnis ist nur ein Verhältnis der tatsächlichen Dämpfung über dem Dämpfungsbetrag, der zum Erreichen der kritischen Dämpfung erforderlich ist. Die Formel für das Dämpfungsverhältnis ( ζ {\displaystyle \zeta }

) des Masse-Feder-Dämpfer-Modells lautet: ζ = c 2 km . {\displaystyle \zeta ={c \über 2{\sqrt {\text{km}}}}.}

Zum Beispiel haben Metallstrukturen (z.B. Flugzeugrümpfe, Motorkurbelwellen) Dämpfungsfaktoren von weniger als 0,05, während Automobilaufhängungen im Bereich von 0,2-0,3 liegen. Die Lösung des unterdämpften Systems für das Masse-Feder-Dämpfer-Modell ist die folgende:
x ( t ) = X e – ζ ω n t cos ( 1 – ζ 2 ω n t – ϕ ) , ω n = 2 π f n . {\displaystyle x(t)=Xe^{-\zeta \omega _{n}t}\cos \left({\sqrt {1-\zeta ^{2}}\omega _{n}t-\phi \right),\qquad \omega _{n}=2\pi f_{n}.}


Der Wert von X, dem Anfangsbetrag, und ϕ , {\displaystyle \phi ,}

die Phasenverschiebung, werden durch den Betrag der Dehnung der Feder bestimmt. Die Formeln für diese Werte finden Sie in den Referenzen.
Gedämpfte und ungedämpfte EigenfrequenzenBearbeiten
Die wichtigsten Punkte, die man bei der Lösung beachten sollte, sind der Exponentialterm und die Kosinusfunktion. Der Exponentialterm definiert, wie schnell das System „abdämpft“ – je größer das Dämpfungsverhältnis, desto schneller dämpft es gegen Null. Die Kosinusfunktion ist der schwingende Anteil der Lösung, aber die Frequenz der Schwingungen ist anders als im ungedämpften Fall.
Die Frequenz in diesem Fall heißt „gedämpfte Eigenfrequenz“, f d , {\displaystyle f_{\text{d}},}

und ist mit der ungedämpften Eigenfrequenz durch folgende Formel verbunden: f d = f n 1 – ζ 2 . {\displaystyle f_{\text{d}}=f_{n}{\sqrt {1-\zeta ^{2}}}.}

Die gedämpfte Eigenfrequenz ist kleiner als die ungedämpfte Eigenfrequenz, aber für viele praktische Fälle ist das Dämpfungsverhältnis relativ klein und daher ist der Unterschied vernachlässigbar. Daher wird bei der Angabe der Eigenfrequenz oft auf die Beschreibung gedämpft und ungedämpft verzichtet (z. B. bei 0,1 Dämpfungsverhältnis ist die gedämpfte Eigenfrequenz nur 1 % kleiner als die ungedämpfte).
Die nebenstehenden Diagramme zeigen, wie sich 0,1 und 0,3 Dämpfungsverhältnisse darauf auswirken, wie das System im Laufe der Zeit „abklingt“. In der Praxis wird häufig die freie Schwingung nach einem Schlag (z. B. mit einem Hammer) experimentell gemessen und dann die Eigenfrequenz des Systems durch Messung der Schwingungsrate sowie das Dämpfungsverhältnis durch Messung der Abklingrate bestimmt. Die Eigenfrequenz und das Dämpfungsverhältnis sind nicht nur bei freien Schwingungen wichtig, sondern charakterisieren auch, wie sich ein System bei erzwungenen Schwingungen verhält.
Zwangsschwingung mit DämpfungBearbeiten
Das Verhalten des Feder-Masse-Dämpfer-Modells ändert sich mit dem Hinzufügen einer harmonischen Kraft. Eine solche Kraft könnte z. B. durch eine rotierende Unwucht erzeugt werden.
F = F 0 sin ( 2 π f t ) . {\displaystyle F=F_{0}\sin(2\pi ft).}

Die Summierung der Kräfte auf die Masse ergibt die folgende gewöhnliche Differentialgleichung:
m x ¨ + c x ˙ + k x = F 0 sin ( 2 π f t ) . {\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F_{0}\sin(2\pi ft).}

Die stationäre Lösung dieses Problems kann geschrieben werden als:
x ( t ) = X sin ( 2 π f t + ϕ ) . {\displaystyle x(t)=X\sin(2\pi ft+\phi ).}

Das Ergebnis besagt, dass die Masse mit der gleichen Frequenz f der angelegten Kraft schwingt, aber mit einer Phasenverschiebung ϕ .
Die Masse schwingt mit der gleichen Frequenz f, aber mit einer Phasenverschiebung ϕ.

Die Amplitude der Schwingung „X“ ist durch folgende Formel definiert.
X = F 0 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 . {\displaystyle X={F_{0} \über k}{1 \über {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}.}

Wobei „r“ definiert ist als das Verhältnis der harmonischen Kraftfrequenz zur ungedämpften Eigenfrequenz des Masse-Feder-Dämpfer-Modells.
r = f f n . {\displaystyle r={\frac {f}{f_{n}}}.}

Die Phasenverschiebung, ϕ , {\displaystyle \phi ,}

ist durch folgende Formel definiert. ϕ = arctan ( – 2 ζ r 1 – r 2 ) . {\displaystyle \phi =\arctan \left({\frac {-2\zeta r}{1-r^{2}}}\right).}


Die Darstellung dieser Funktionen, genannt „Frequenzgang des Systems“, stellt eines der wichtigsten Merkmale bei erzwungenen Schwingungen dar. In einem leicht gedämpften System, wenn die erzwungene Frequenz sich der Eigenfrequenz nähert ( r ≈ 1 {\displaystyle r\approx 1}

) kann die Amplitude der Schwingung extrem hoch werden. Dieses Phänomen wird als Resonanz bezeichnet (in der Folge wird die Eigenfrequenz eines Systems oft als Resonanzfrequenz bezeichnet). In Rotorlagersystemen wird jede Drehzahl, die eine Resonanzfrequenz anregt, als kritische Drehzahl bezeichnet.
Wenn in einem mechanischen System Resonanz auftritt, kann dies sehr schädlich sein – bis hin zum Ausfall des Systems. Daher ist einer der Hauptgründe für die Schwingungsanalyse die Vorhersage, wann diese Art von Resonanz auftreten kann und welche Maßnahmen zu ergreifen sind, um das Auftreten zu verhindern. Wie das Amplituden-Diagramm zeigt, kann das Hinzufügen von Dämpfung die Größe der Schwingung erheblich reduzieren. Die Größe kann auch verringert werden, wenn die Eigenfrequenz durch Änderung der Steifigkeit oder Masse des Systems von der erzwungenen Frequenz weg verschoben werden kann. Wenn das System nicht verändert werden kann, kann vielleicht die erzwungene Frequenz verschoben werden (z. B. durch Änderung der Geschwindigkeit der Maschine, die die Kraft erzeugt).
Im Folgenden werden einige weitere Punkte in Bezug auf die erzwungene Schwingung in den Frequenzgangdiagrammen dargestellt.
- Bei einem gegebenen Frequenzverhältnis ist die Amplitude der Schwingung, X, direkt proportional zur Amplitude der Kraft F 0 {\displaystyle F_{0}}
(z.B.. wenn Sie die Kraft verdoppeln, verdoppelt sich die Schwingung)
- Bei geringer oder keiner Dämpfung ist die Schwingung phasengleich mit der erzwungenen Frequenz, wenn das Frequenzverhältnis r < 1 ist, und um 180 Grad phasenverschoben, wenn das Frequenzverhältnis r > 1 ist
- Wenn r ≪ 1 ist, ist die Amplitude gerade die Auslenkung der Feder unter der statischen Kraft F 0. Displaystyle F_{0}.
Diese Auslenkung nennt man die statische Auslenkung δ s t . δ s t.
Wenn also r ≪ 1 ist, sind die Auswirkungen des Dämpfers und der Masse minimal.
- Wenn r ≫ 1 ist, ist die Amplitude der Schwingung tatsächlich kleiner als die statische Auslenkung δ s t .
- Ungeachtet der Dämpfung ist die Schwingung um 90 Grad phasenverschoben mit der Antriebsfrequenz, wenn das Frequenzverhältnis r = 1 ist, was sehr hilfreich ist, wenn es um die Bestimmung der Eigenfrequenz des Systems geht.
- Unabhängig von der Dämpfung ist die Schwingung bei r ≫ 1 um 180 Grad phasenverschoben zur erzwungenen Frequenz
- Unabhängig von der Dämpfung ist die Schwingung bei r ≪ 1 phasengleich mit der erzwungenen Frequenz
.

In diesem Bereich ist die von der Masse erzeugte Kraft (F = ma) dominierend, da die von der Masse wahrgenommene Beschleunigung mit der Frequenz zunimmt. Da die Auslenkung der Feder, X, in diesem Bereich reduziert ist, wird die Kraft, die von der Feder (F = kx) auf die Basis übertragen wird, reduziert. Daher isoliert das Masse-Feder-Dämpfer-System die Oberwellenkraft von der Montagebasis – man spricht von Schwingungsisolierung. Mehr Dämpfung verringert die Wirkung der Schwingungsisolierung, wenn r ≫ 1 ist, weil die Dämpfungskraft (F = cv) auch auf die Basis übertragen wird.
Resonanzursachen
Resonanz ist einfach zu verstehen, wenn man die Feder und die Masse als Energiespeicherelemente betrachtet – wobei die Masse kinetische Energie und die Feder potentielle Energie speichert. Wie bereits erwähnt, übertragen Masse und Feder, wenn keine äußere Kraft auf sie einwirkt, Energie mit einer Rate, die der Eigenfrequenz entspricht, hin und her. Mit anderen Worten, um effizient Energie in Masse und Feder zu pumpen, muss die Energiequelle die Energie mit einer Rate einspeisen, die der Eigenfrequenz entspricht. Das Aufbringen einer Kraft auf die Masse und die Feder ist vergleichbar mit dem Schieben eines Kindes auf der Schaukel, ein Schubs ist im richtigen Moment erforderlich, damit die Schaukel höher und höher wird. Wie im Fall der Schaukel muss die aufgebrachte Kraft nicht hoch sein, um große Bewegungen zu erhalten, sondern dem System nur Energie hinzufügen.
Der Dämpfer speichert keine Energie, sondern gibt Energie ab. Da die Dämpfungskraft proportional zur Geschwindigkeit ist, dissipiert der Dämpfer umso mehr Energie, je größer die Bewegung ist. Daher gibt es einen Punkt, an dem die vom Dämpfer abgeleitete Energie gleich der durch die Kraft zugeführten Energie ist. An diesem Punkt hat das System seine maximale Amplitude erreicht und wird auf diesem Niveau weiterschwingen, solange die aufgebrachte Kraft gleich bleibt. Wenn keine Dämpfung vorhanden ist, gibt es nichts, um die Energie zu zerstreuen, und die Bewegung wächst theoretisch weiter ins Unendliche.
Anwendung „komplexer“ Kräfte auf das Masse-Feder-Dämpfer-ModellBearbeiten
In einem vorherigen Abschnitt wurde nur eine einfache harmonische Kraft auf das Modell angewendet, aber dies kann mit zwei leistungsstarken mathematischen Werkzeugen erheblich erweitert werden. Das erste ist die Fourier-Transformation, die ein Signal als Funktion der Zeit (Zeitbereich) nimmt und es in seine harmonischen Komponenten als Funktion der Frequenz (Frequenzbereich) zerlegt. Zum Beispiel, indem man eine Kraft auf das Masse-Feder-Dämpfer-Modell anwendet, die den folgenden Zyklus wiederholt – eine Kraft gleich 1 Newton für 0,5 Sekunden und dann keine Kraft für 0,5 Sekunden. Diese Art von Kraft hat die Form einer 1-Hz-Rechteckwelle.
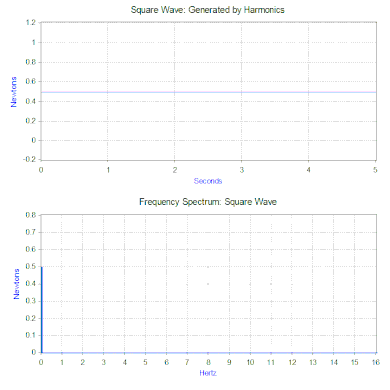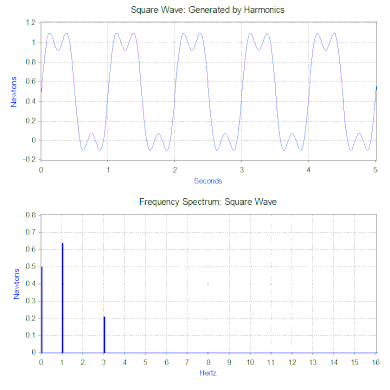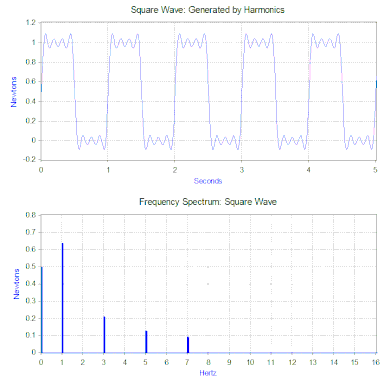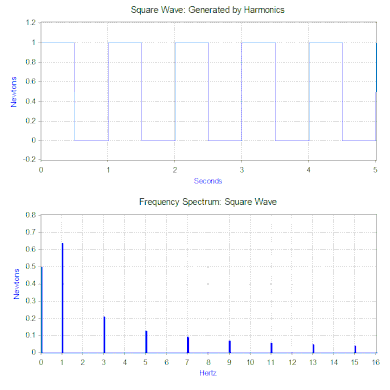
Die Fourier-Transformation der Rechteckwelle erzeugt ein Frequenzspektrum, das die Größe der Oberschwingungen, aus denen die Rechteckwelle besteht, darstellt (die Phase wird ebenfalls erzeugt, ist aber typischerweise von geringerer Bedeutung und wird daher oft nicht aufgezeichnet). Die Fourier-Transformation kann auch verwendet werden, um nicht-periodische Funktionen wie Transienten (z. B. Impulse) und Zufallsfunktionen zu analysieren. Die Fourier-Transformation wird fast immer mit dem Computer-Algorithmus der schnellen Fourier-Transformation (FFT) in Kombination mit einer Fensterfunktion berechnet.
Im Fall unserer Rechteckkraft ist die erste Komponente tatsächlich eine konstante Kraft von 0,5 Newton und wird durch einen Wert bei 0 Hz im Frequenzspektrum dargestellt. Die nächste Komponente ist eine 1-Hz-Sinuswelle mit einer Amplitude von 0,64. Diese wird durch die Linie bei 1 Hz dargestellt. Die restlichen Komponenten liegen bei ungeraden Frequenzen und es sind unendlich viele Sinuswellen nötig, um die perfekte Rechteckwelle zu erzeugen. Daher erlaubt die Fourier-Transformation, die Kraft als eine Summe von Sinuskräften zu interpretieren, die anstelle einer „komplexeren“ Kraft (z. B. einer Rechteckwelle) aufgebracht werden.
Im vorherigen Abschnitt wurde die Schwingungslösung für eine einzelne harmonische Kraft angegeben, aber die Fourier-Transformation ergibt im Allgemeinen mehrere harmonische Kräfte. Das zweite mathematische Hilfsmittel, das „Überlagerungsprinzip“, erlaubt die Summierung der Lösungen von mehreren Kräften, wenn das System linear ist. Im Fall des Feder-Masse-Dämpfer-Modells ist das System linear, wenn die Federkraft proportional zur Verschiebung und die Dämpfung proportional zur Geschwindigkeit über den interessierenden Bewegungsbereich ist. Daher ist die Lösung des Problems mit einer Rechteckwelle die Summierung der vorhergesagten Schwingung von jeder einzelnen der harmonischen Kräfte, die im Frequenzspektrum der Rechteckwelle gefunden werden.
FrequenzgangmodellBearbeiten
Die Lösung eines Schwingungsproblems kann als eine Eingabe/Ausgabe-Beziehung betrachtet werden – wobei die Kraft die Eingabe und die Ausgabe die Schwingung ist. Die Darstellung von Kraft und Schwingung im Frequenzbereich (Betrag und Phase) ermöglicht folgende Beziehung:
X ( i ω ) = H ( i ω ) ⋅ F ( i ω ) oder H ( i ω ) = X ( i ω ) F ( i ω ) . {\displaystyle X(i\omega )=H(i\omega )\cdot F(i\omega ){\text{ oder }}H(i\omega )={X(i\omega ) \über F(i\omega )}.}

H ( i ω ) {\displaystyle H(i\omega )}

wird als Frequenzgangfunktion bezeichnet (auch Übertragungsfunktion genannt, aber technisch nicht so genau) und hat sowohl eine Betrags- als auch eine Phasenkomponente (bei Darstellung als komplexe Zahl eine reelle und imaginäre Komponente). Der Betrag der Frequenzgangfunktion (FRF) wurde bereits für das Masse-Feder-Dämpfer-System dargestellt. | H ( i ω ) | = | X ( i ω ) F ( i ω ) | = 1 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 , wobei r = f f n = ω ω n . {\displaystyle |H(i\omega )|=\left|{X(i\omega ) \over F(i\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},{\text{ wobei }}r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}.}

Die Phase der FRF wurde früher auch dargestellt als:
∠ H ( i ω ) = – arctan ( 2 ζ r 1 – r 2 ) . ∠ H ( i ω ) = – arctan ( 2 ζ r 1 – r 2 ) .


Bei der Berechnung der FRF für ein Masse-Feder-Dämpfer-System mit einer Masse von 1 kg, einer Federsteifigkeit von 1.93 N/mm und einem Dämpfungsverhältnis von 0,1. Die Werte der Feder und der Masse ergeben für dieses spezifische System eine Eigenfrequenz von 7 Hz. Die Anwendung der 1-Hz-Rechteckwelle von vorhin ermöglicht die Berechnung der vorhergesagten Schwingung der Masse. Die Abbildung veranschaulicht die resultierende Schwingung. In diesem Beispiel ist es so, dass die vierte Harmonische der Rechteckwelle auf 7 Hz fällt. Der Frequenzgang des Masse-Feder-Dämpfers gibt daher eine hohe 7-Hz-Schwingung aus, obwohl die Eingangskraft eine relativ niedrige 7-Hz-Oberschwingung hatte. Dieses Beispiel verdeutlicht, dass die resultierende Schwingung sowohl von der Antriebsfunktion als auch von dem System abhängt, auf das die Kraft ausgeübt wird.
Die Abbildung zeigt auch die Zeitbereichsdarstellung der resultierenden Schwingung. Dazu wird eine inverse Fourier-Transformation durchgeführt, die Daten aus dem Frequenzbereich in den Zeitbereich umwandelt. In der Praxis wird dies selten durchgeführt, da das Frequenzspektrum alle notwendigen Informationen liefert.
Die Frequenzgangfunktion (FRF) muss nicht unbedingt aus der Kenntnis der Masse, Dämpfung und Steifigkeit des Systems berechnet werden, sondern kann experimentell gemessen werden. Wird z. B. eine bekannte Kraft über einen Frequenzbereich aufgebracht und werden die zugehörigen Schwingungen gemessen, kann die Frequenzgangfunktion berechnet und damit das System charakterisiert werden. Diese Technik wird im Bereich der experimentellen Modalanalyse eingesetzt, um die Schwingungseigenschaften einer Struktur zu bestimmen.
>.

