Negatives Binomial-Experiment / Verteilung: Definition, Beispiele

Binomialtheorem > Negativer Binomialsatz

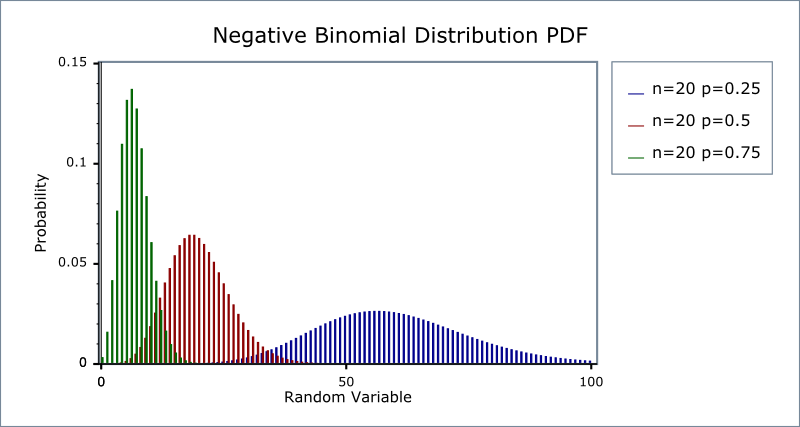
Bild: UCSF

Das negative Binomial-Experiment ist fast dasselbe wie ein Binomial-Experiment mit einem Unterschied: Ein Binomial-Experiment hat eine feste Anzahl von Versuchen.

Wenn die folgenden fünf Bedingungen wahr sind, ist das Experiment binomial:

1. Feste Anzahl von n Versuchen.
2. Jeder Versuch ist unabhängig.
3. Nur zwei Ergebnisse sind möglich (Erfolg und Misserfolg).
4. Die Erfolgswahrscheinlichkeit (p) für jeden Versuch ist konstant.
5. Eine Zufallsvariable Y= die Anzahl der Erfolge.

Beispiel: Nehmen Sie ein Standard-Kartenspiel, mischen Sie es und wählen Sie eine Karte aus. Ersetzen Sie die Karte und wiederholen Sie dies zwanzigmal. Y ist die Anzahl der Asse, die Sie ziehen.

Das negative Binom ähnelt dem Binom mit zwei Unterschieden (speziell zu den Nummern 1 und 5 in der obigen Liste):

• Die Anzahl der Versuche, n ist nicht festgelegt.
• Eine Zufallsvariable Y= die Anzahl der Versuche, die benötigt werden, um r Erfolge zu erzielen.

Beispiel: Nehmen Sie ein Standard-Kartenspiel, mischen Sie es und wählen Sie eine Karte. Ersetzen Sie die Karte und wiederholen Sie den Vorgang, bis Sie zwei Asse gezogen haben. Y ist die Anzahl der Versuche, die benötigt werden, um zwei Asse zu ziehen. Da die Anzahl der Versuche nicht festgelegt ist (d. h. Sie hören auf, wenn Sie das zweite Ass ziehen), handelt es sich um eine negative Binomialverteilung.

Was ist eine negative Binomialverteilung?

Eine negative Binomialverteilung (auch Pascalsche Verteilung genannt) ist eine diskrete Wahrscheinlichkeitsverteilung für Zufallsvariablen in einem negativen Binomialversuch.

Die Zufallsvariable ist die Anzahl der wiederholten Versuche, X, die eine bestimmte Anzahl von Erfolgen, r, hervorbringen, also die Anzahl der Misserfolge vor einem Erfolg. Dies ist der Hauptunterschied zur Binomialverteilung: Bei einer regulären Binomialverteilung betrachtet man die Anzahl der Erfolge. Bei einer negativen Binomialverteilung zählt die Anzahl der Misserfolge.

Warum heißt sie Negative Binomialverteilung?

Wenn Sie den Begriff „negativ“ hören, denken Sie vielleicht, dass eine positive Verteilung auf der x-Achse umgedreht wird, wodurch sie negativ wird. Der „negative“ Teil der negativen Binomialverteilung rührt jedoch tatsächlich von der Tatsache her, dass eine Facette der Binomialverteilung umgekehrt wird: In einem Binomialexperiment zählen Sie die Anzahl der Erfolge in einer festen Anzahl von Versuchen; im obigen Beispiel zählen Sie, wie viele Asse Sie ziehen. Bei einem negativen Binomial-Experiment zählen Sie die Misserfolge, oder wie viele Karten Sie brauchen, um zwei Asse zu ziehen.

Die negative Binomialformel

Wahrscheinlichkeit:
b*(x; r, P) = x-1Cr-1 * Pr * (1 – P)x – r
mit x=Anzahl der Versuche
r = Erfolge

Mittelwert:
μ = r / P
wobei r die Anzahl der Versuche ist
P=Erfolgswahrscheinlichkeit für jeden Versuch

Lösen von Problemen mit negativem Binomialversuch

Die pmf für die negative Binomialverteilung ist: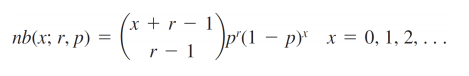

Wobei:
r die Anzahl der Erfolge und
p = die Erfolgswahrscheinlichkeit ist.

Beispielfrage: Sie befragen Personen, die aus einer Wahlkabine kommen, und fragen sie, ob sie unabhängig gewählt haben. Die Wahrscheinlichkeit (p), dass eine Person unabhängig gewählt hat, beträgt 20%. Wie hoch ist die Wahrscheinlichkeit, dass 15 Personen befragt werden müssen, bevor Sie 5 Personen finden, die unabhängig gewählt haben?

Schritt 1: Finden Sie p, r und X.
Wir erhalten (in der Frage), dass p = 20%(.2) und r = 5. Die Anzahl der Ausfälle, X, ist 15 – 5 = 10.

Schritt 2: Setzen Sie diese Werte aus Schritt 1 in die Formel ein:

Schritt 3: Lösen Sie. Der erste Teil (14 über 4) ist eine Kombination (verwenden Sie unseren Kombinationsrechner, um 14 zu finden, wählen Sie 4).
1001*.25*.810 = 0.034.

Die Wahrscheinlichkeit, dass Sie 15 Leute fragen müssen, um 5 Stimmen für unabhängig zu bekommen, ist .034, oder 3.4%.

Die geometrische Verteilung ist ein Spezialfall der negativen Binomialverteilung.

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf dem Gebiet erhalten. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!