De Stellingen van DeMorgan

Een wiskundige genaamd DeMorgan ontwikkelde een paar belangrijke regels met betrekking tot groepscomplementatie in Booleaanse algebra.

Met groepscomplementatie bedoel ik het complement van een groep termen, voorgesteld door een lange balk over meer dan één variabele.

U herinnert zich nog wel uit het hoofdstuk over logische poorten dat het omkeren van alle ingangen van een poort de essentiële functie van die poort omkeert van AND naar OR, of omgekeerd, en ook de uitgang omkeert.

Dus een OR poort met alle ingangen geïnverteerd (een Negative-OR poort) gedraagt zich hetzelfde als een NAND poort, en een AND poort met alle ingangen geïnverteerd (een Negative-AND poort) gedraagt zich hetzelfde als een NOR poort.

DeMorgan’s stellingen stellen dezelfde equivalentie in “achterwaartse” vorm: dat het inverteren van de uitgang van een willekeurige poort resulteert in dezelfde functie als het tegenovergestelde type van de poort (AND vs. OR) met geïnverteerde ingangen:

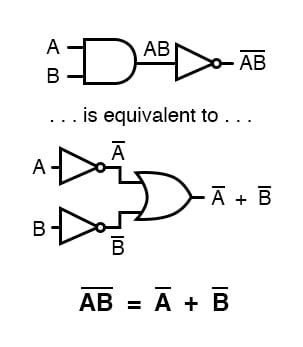
Een lange balk die zich uitstrekt over de term AB fungeert als een groeperingssymbool, en is als zodanig geheel anders dan het product van A en B onafhankelijk geïnverteerd.

Met andere woorden, (AB)’ is niet gelijk aan A’B’. Omdat het “priem”-symbool (‘) niet over twee variabelen kan worden uitgerekt zoals een balk dat kan, zijn we genoodzaakt haakjes te gebruiken om het van toepassing te laten zijn op de hele term AB in de vorige zin.

Een staaf fungeert echter als zijn eigen groeperingssymbool wanneer hij over meer dan één variabele wordt uitgerekt.

Dit heeft ingrijpende gevolgen voor de manier waarop Booleaanse uitdrukkingen worden geëvalueerd en gereduceerd, zoals we zullen zien.

De stelling van DeMorgan

De stelling van DeMorgan kan worden opgevat als het breken van een lange staafsymbool.

Wanneer een lange staaf wordt gebroken, verandert de bewerking direct onder de breuk van optellen in vermenigvuldigen, of omgekeerd, en de gebroken stukken staaf blijven over de afzonderlijke variabelen liggen. Ter illustratie:

Wanneer een uitdrukking meerdere “lagen” van staven bevat, mag u slechts één staaf tegelijk breken, en is het over het algemeen eenvoudiger om de vereenvoudiging te beginnen door eerst de langste (bovenste) staaf te breken.

Om dit te illustreren, nemen we de uitdrukking (A + (BC)’)’ en vereenvoudigen we deze met behulp van DeMorgan’s Stellingen:

Naar het advies om eerst de langste (bovenste) staaf te breken, begin ik als eerste stap met het breken van de staaf die de hele uitdrukking omvat:

Hieruit volgt dat de oorspronkelijke schakeling wordt gereduceerd tot een drie-ingangs AND-poort met de A-ingang geïnverteerd:

U moet nooit meer dan één staaf in één stap breken, zoals hier geïllustreerd:

Hoe verleidelijk het ook mag zijn om stappen te besparen en meer dan één staaf tegelijk te breken, het leidt vaak tot een onjuist resultaat, dus doe het niet!

Het is mogelijk om deze uitdrukking op de juiste manier te verkleinen door eerst de korte staaf te breken, in plaats van eerst de lange:

Het eindresultaat is hetzelfde, maar er zijn meer stappen nodig vergeleken met de eerste methode, waarbij de langste staaf eerst werd gebroken.

Merk op hoe we in de derde stap de lange staaf op twee plaatsen hebben gebroken.

Dit is een legitieme wiskundige bewerking, en niet hetzelfde als het breken van twee staven in één stap!

Het verbod op het breken van meer dan één staaf in één stap is geen verbod op het breken van een staaf op meer dan één plaats.

Het breken op meer dan één plaats in één stap is toegestaan; het breken van meer dan één staaf in één stap is dat niet.

Je vraagt je misschien af waarom er haakjes rond de sub-expressie B’ + C’ zijn geplaatst, gezien het feit dat ik ze in de volgende stap juist heb verwijderd.

Ik heb dit gedaan om een belangrijk maar gemakkelijk te veronachtzamen aspect van DeMorgan’s stelling te benadrukken.

Omdat een lange balk als groeperingssymbool fungeert, moeten de variabelen die voorheen door een gebroken balk werden gegroepeerd, gegroepeerd blijven, anders gaat de juiste rangorde (volgorde van bewerking) verloren.

In dit voorbeeld zou het niet erg zijn als ik vergat haakjes in te voegen na het breken van de korte balk, maar in andere gevallen zou dat wel kunnen.

Kijk eens naar dit voorbeeld, dat begint met een andere uitdrukking:

Zoals u ziet, is het behoud van de groepering die wordt geïmpliceerd door de complementatiebalken voor deze uitdrukking van cruciaal belang voor het verkrijgen van het juiste antwoord.

Laten we de principes van DeMorgan’s stellingen toepassen op de vereenvoudiging van een poortschakeling:

Zoals altijd moet onze eerste stap bij het vereenvoudigen van deze schakeling bestaan uit het genereren van een equivalente Booleaanse uitdrukking.

Dit kunnen we doen door een label voor een sub-uitdrukking te plaatsen bij de uitgang van elke poort, naarmate de ingangen bekend worden. Dit is de eerste stap in dit proces:

Volgende stap is het labelen van de uitgangen van de eerste NOR-poort en de NAND-poort.

Wanneer we te maken hebben met poorten met een geïnverteerde uitgang, vind ik het eenvoudiger om een uitdrukking te schrijven voor de uitgang van de poort zonder de uiteindelijke inversie, met een pijl die wijst naar net voor de inversie-bel.

Dan, op de draad die uit de poort komt (na de bel), schrijf ik de volledige, aangevulde uitdrukking.

Dit helpt voorkomen dat ik een complementaire staaf in de subuitdrukking vergeet, doordat ik mezelf dwing de taak van het schrijven van de uitdrukking in twee stappen op te splitsen:

Tot slot schrijven we een uitdrukking (of een paar uitdrukkingen) voor de laatste NOR-poort:

Nu reduceren we deze uitdrukking met behulp van de identiteiten, eigenschappen, regels en stellingen (DeMorgan’s) van de Booleaanse algebra:

De equivalente poortschakeling voor deze sterk vereenvoudigde uitdrukking ziet er als volgt uit:

REVIEW:

• De stellingen van DeMorgan beschrijven de gelijkwaardigheid tussen poorten met geïnverteerde ingangen en poorten met geïnverteerde uitgangen. Eenvoudig gezegd, een NAND poort is equivalent aan een Negatieve-OR poort, en een NOR poort is equivalent aan een Negatieve-AND poort.
• Bij het “breken” van een complementatiestaaf in een Booleaanse uitdrukking, keert de bewerking direct onder de breuk (optellen of vermenigvuldigen) om, en blijven de gebroken staafdelen over de respectievelijke termen.
• Het is vaak gemakkelijker om een probleem te benaderen door de langste (bovenste) staaf te breken, voordat je eronder een staaf breekt. U moet nooit proberen om twee balken in één stap te breken!
• Complementatiebalken functioneren als groeperingssymbolen. Daarom moeten, wanneer een balk wordt afgebroken, de termen eronder gegroepeerd blijven. Rond deze gegroepeerde termen kunnen haakjes worden geplaatst als hulp om te voorkomen dat de rangorde verandert.