Jacobiaan

Gegeven een verzameling van vergelijkingen in variabelen , expliciet geschreven als

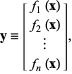(1)

of explicieter als

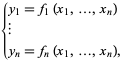(2)

de Jacobiaanse matrix, soms eenvoudigweg “de Jacobiaan” genoemd (Simon en Blume 1994) is gedefinieerd door

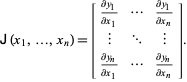(3)

De determinant van is de Jacobiaanse determinant (verwarrend, ook vaak “de Jacobiaan” genoemd) en wordt aangeduid

(4)

De Jacobiaanse matrix en determinant kunnen in de WolframLanguage worden berekend met

 JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})

Het nemen van de differentiaal

(5)

blijkt dat de determinant is van de matrix , en geeft dus de verhoudingen van -dimensionale volumes (inhoud) in en ,

(6)

Het komt dus bijvoorbeeld voor in de variabelenwisseltheorema.

Het concept van de Jacobiaan kan ook worden toegepast op functies in meer dan variabelen. Bijvoorbeeld, als we en beschouwen, de Jacobianen

			(7)
			(8)

kan worden gedefinieerd (Kaplan 1984, p. 99).

Voor het geval van variabelen heeft de Jacobiaan de speciale vorm

(9)

waar het scalair product is en het crossproduct is, die kan worden uitgebreid tot

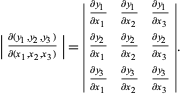(10)