Efekt Dopplera
Akustyczny dopplerowski profiler prąduEdit
Akustyczny dopplerowski profiler prądu (ADCP) jest hydroakustycznym miernikiem prądu podobnym do sonaru, używanym do pomiaru prędkości prądu wody w zakresie głębokości z wykorzystaniem efektu Dopplera fal dźwiękowych rozproszonych z powrotem od cząstek w słupie wody. Termin ADCP jest ogólnym określeniem dla wszystkich akustycznych profilerów prądowych, chociaż skrót pochodzi od serii instrumentów wprowadzonych przez RD Instruments w latach 80-tych. Zakres częstotliwości roboczych ADCP mieści się w przedziale od 38 kHz do kilku megaherców. Urządzenie używane w powietrzu do profilowania prędkości wiatru za pomocą dźwięku znane jest jako SODAR i działa na tych samych zasadach.
RobotykaEdit
Dynamiczne planowanie ścieżki w czasie rzeczywistym w robotyce, aby wspomóc ruch robotów w skomplikowanym środowisku z ruchomymi przeszkodami często korzysta z efektu Dopplera. Takie aplikacje są szczególnie wykorzystywane w robotyce konkurencyjnej, gdzie środowisko ciągle się zmienia, np. w piłce nożnej.
SyrenyEdit

Odtwórz media
Syrena na przejeżdżającym pojeździe ratunkowym rozpocznie się wyżej niż jej stacjonarne nachylenie, zsunie się w dół, gdy przejedzie, i będzie kontynuowana niżej niż jej stacjonarne nachylenie, gdy oddali się od obserwatora. Astronom John Dobson wyjaśnił ten efekt w następujący sposób:
Powodem, dla którego syrena się ślizga, jest to, że nie uderza w ciebie.
Innymi słowy, gdyby syrena zbliżyła się bezpośrednio do obserwatora, jej wysokość pozostałaby stała, wyższa niż wysokość stacjonarna, dopóki pojazd nie uderzyłby w niego, a następnie natychmiast skoczyłaby do nowej, niższej wysokości. Ponieważ pojazd przejeżdża obok obserwatora, prędkość radialna nie pozostaje stała, lecz zmienia się jako funkcja kąta pomiędzy jego linią wzroku a prędkością syreny:
v radial = v s ⋅ cos θ {displaystyle v_{text{radial}}=v_{text{s}}}cdot ⋅ cos θ }}

gdzie θ {{displaystyle θ}}.

jest kątem między prędkością postępową obiektu a linią widzenia od obiektu do obserwatora.
AstronomyEdit
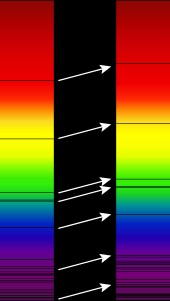
Efekt Dopplera dla fal elektromagnetycznych, takich jak światło, jest bardzo przydatny w astronomii i skutkuje tak zwanym przesunięciem ku czerwieni (redshift) lub przesunięciem ku błękitowi (blueshift). Został on wykorzystany do pomiaru prędkości, z jaką gwiazdy i galaktyki zbliżają się lub oddalają od nas, czyli ich prędkości radialnych. Może to być wykorzystane do wykrycia, czy pozornie pojedyncza gwiazda jest w rzeczywistości bliskim układem podwójnym, do pomiaru prędkości rotacji gwiazd i galaktyk lub do wykrywania egzoplanet. Ten redshift i blueshift zachodzi w bardzo małej skali. Jeśli obiekt poruszałby się w kierunku Ziemi, nie byłoby zauważalnej różnicy w świetle widzialnym, dla niewprawnego oka.
Zauważ, że przesunięcie ku czerwieni jest również używane do pomiaru ekspansji przestrzeni, ale nie jest to tak naprawdę efekt Dopplera. Przesunięcie ku czerwieni spowodowane rozszerzaniem się przestrzeni jest znane jako przesunięcie kosmologiczne, które może być wyprowadzone wyłącznie z metryki Robertsona-Walkera w ramach formalizmu ogólnej teorii względności. Zdarza się również, że w skalach kosmologicznych występują wykrywalne efekty Dopplera, które, jeśli są błędnie interpretowane jako kosmologiczne, prowadzą do obserwacji zniekształceń przestrzeni redshiftu.
Użycie efektu Dopplera dla światła w astronomii zależy od naszej wiedzy, że widma gwiazd nie są jednorodne. Wykazują one linie absorpcyjne o dobrze zdefiniowanych częstotliwościach, które są skorelowane z energiami wymaganymi do wzbudzenia elektronów w różnych pierwiastkach z jednego poziomu na drugi. Efekt Dopplera można rozpoznać po tym, że linie absorpcyjne nie zawsze mają częstotliwości, które uzyskuje się z widma stacjonarnego źródła światła. Ponieważ światło niebieskie ma wyższą częstotliwość niż światło czerwone, linie widmowe zbliżającego się astronomicznego źródła światła wykazują przesunięcie ku błękitowi, a linie widmowe oddalającego się astronomicznego źródła światła wykazują przesunięcie ku czerwieni.
Wśród pobliskich gwiazd, największe prędkości radialne względem Słońca wynoszą +308 km/s (BD-15°4041, znana również jako LHS 52, odległa o 81,7 lat świetlnych) oraz -260 km/s (Woolley 9722, znana również jako Wolf 1106 i LHS 64, odległa o 78,2 lat świetlnych). Dodatnia prędkość radialna oznacza, że gwiazda oddala się od Słońca, ujemna, że się zbliża.
RadarEdit
Efekt Dopplera jest wykorzystywany w niektórych rodzajach radarów, do pomiaru prędkości wykrywanych obiektów. Wiązka radaru jest wystrzeliwana na poruszający się cel – np. samochód, ponieważ policja używa radaru do wykrywania kierowców przekraczających prędkość – w miarę jak zbliża się on lub oddala od źródła radaru. Każda kolejna fala radarowa musi przebyć dalszą drogę, aby dotrzeć do samochodu, zanim zostanie odbita i ponownie wykryta w pobliżu źródła. Ponieważ każda fala musi poruszać się dalej, zwiększa się odstęp pomiędzy poszczególnymi falami, co zwiększa długość fali. W niektórych sytuacjach wiązka radaru jest wystrzeliwana w kierunku poruszającego się samochodu, gdy ten się zbliża, w którym to przypadku każda kolejna fala pokonuje mniejszą odległość, zmniejszając długość fali. W obu przypadkach obliczenia na podstawie efektu Dopplera pozwalają dokładnie określić prędkość samochodu. Co więcej, zapalnik zbliżeniowy, opracowany w czasie II wojny światowej, opiera się na radarze dopplerowskim, aby zdetonować materiały wybuchowe w odpowiednim czasie, na odpowiedniej wysokości, w odpowiedniej odległości itd.
Ponieważ przesunięcie dopplerowskie wpływa zarówno na falę padającą na cel, jak i na falę odbitą z powrotem do radaru, zmiana częstotliwości obserwowana przez radar z powodu celu poruszającego się z prędkością względną Δ v {Delta v}

jest dwa razy większa niż w przypadku tego samego celu emitującego falę: Δ f = 2 Δ v c f 0 {{displaystyle ΔDelta f={frac {2Delta v}{c}}f_{0}}}.

.
MedicalEdit

Echokardiogram może, w pewnych granicach, uzyskać dokładną ocenę kierunku przepływu krwi oraz prędkości krwi i tkanki mięśnia sercowego w dowolnym arbitralnie wybranym punkcie z wykorzystaniem efektu Dopplera. Jednym z ograniczeń jest to, że wiązka ultradźwiękowa powinna być jak najbardziej równoległa do przepływu krwi. Pomiar prędkości pozwala na ocenę powierzchni i funkcji zastawek serca, zaburzeń komunikacji pomiędzy lewą i prawą stroną serca, przeciekania krwi przez zastawki (niedomykalność zastawek) oraz na obliczenie rzutu serca. Ultrasonografia wzmacniana kontrastem przy użyciu wypełnionych gazem mikropęcherzyków może być wykorzystywana do poprawy pomiarów prędkości i innych pomiarów medycznych związanych z przepływem.
Ale chociaż „Doppler” stał się synonimem „pomiaru prędkości” w obrazowaniu medycznym, w wielu przypadkach nie mierzy się przesunięcia częstotliwości (przesunięcia dopplerowskiego) odbieranego sygnału, ale przesunięcie fazy (kiedy dociera odbierany sygnał).
Pomiary prędkości przepływu krwi są również stosowane w innych dziedzinach ultrasonografii medycznej, takich jak ultrasonografia położnicza i neurologia. Pomiar prędkości przepływu krwi w tętnicach i żyłach w oparciu o efekt Dopplera jest skutecznym narzędziem do diagnozowania problemów naczyniowych, takich jak zwężenia.
Pomiar przepływuEdit
Przyrządy takie jak laserowy welocimetr dopplerowski (LDV) i akustyczny welocimetr dopplerowski (ADV) zostały opracowane do pomiaru prędkości w przepływie cieczy. LDV emituje wiązkę światła, a ADV emituje ultradźwiękowy impuls akustyczny i mierzy przesunięcie dopplerowskie w długościach fal odbić od cząstek poruszających się z przepływem. Rzeczywisty przepływ jest obliczany jako funkcja prędkości i fazy wody. Technika ta pozwala na nieinwazyjne pomiary przepływu, z wysoką precyzją i częstotliwością.
Pomiar profilu prędkości
Opracowana pierwotnie do pomiarów prędkości w zastosowaniach medycznych (przepływ krwi), Ultradźwiękowa Velocimetria Dopplerowska (UDV) może mierzyć w czasie rzeczywistym pełny profil prędkości w prawie każdej cieczy zawierającej cząstki w zawiesinie, takie jak pył, pęcherzyki gazu, emulsje. Przepływy mogą być pulsujące, oscylujące, laminarne lub turbulentne, stacjonarne lub przejściowe. Technika ta jest w pełni nieinwazyjna.
SatelityEdit
 Możliwe przesunięcia dopplerowskie w zależności od kąta elewacji (LEO: wysokość orbitalna h {\i0}
 = 750 km). Stała stacja naziemna. |
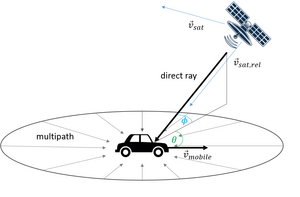 Geometria dla efektów Dopplera. Zmienne: v m o b {{displaystyle v_{mob}}
 jest prędkością stacji ruchomej, v S a t {{displaystyle v_{Sat}}  to prędkość satelity, v r e l , s a t {{displaystyle v_{rel,sat}}  to prędkość względna satelity, ϕ {{displaystyle phi }  to kąt elewacji satelity, a θ {displaystyle \theta }  jest kierunkiem jazdy w stosunku do satelity. |
 Efekt Dopplera na kanale ruchomym. Zmienne: f c = c λ c {{displaystyle f_{c}}={frac {c}}{{lambda {{rm {c}}}}}
 jest częstotliwością nośną, f D , m a x = v m o b λ c {{displaystyle f_{rm {D,max}}={{frac {v_{rm {mob}}}{{lambda _{lambda {c}}}}}  jest maksymalnym przesunięciem dopplerowskim spowodowanym przez poruszającą się stację ruchomą (patrz Doppler Spread), a f D , S a t {\displaystyle f_{\rm {D,Sat}}  jest dodatkowym przesunięciem dopplerowskim spowodowanym ruchem satelity. |
Nawigacja satelitarnaEdit
Przesunięcie dopplerowskie może być wykorzystane do nawigacji satelitarnej, takiej jak w systemach Transit i DORIS.
Komunikacja satelitarnaEdit
Doppler również musi być kompensowany w komunikacji satelitarnej. Szybko poruszające się satelity mogą mieć przesunięcie dopplerowskie rzędu kilkudziesięciu kiloherców względem stacji naziemnej. Prędkość, a tym samym wielkość efektu Dopplera, zmienia się z powodu krzywizny ziemi. Aby satelita otrzymywał sygnał o stałej częstotliwości, stosuje się dynamiczną kompensację dopplerowską, w której częstotliwość sygnału jest stopniowo zmieniana podczas transmisji. Po uświadomieniu sobie, że przesunięcie dopplerowskie nie zostało uwzględnione przed wystrzeleniem sondy Huygens w ramach misji Cassini-Huygens w 2005 roku, zmieniono trajektorię sondy tak, aby zbliżała się do Tytana w taki sposób, aby transmisje odbywały się prostopadle do kierunku jej ruchu względem Cassiniego, co znacznie zmniejszyło przesunięcie dopplerowskie.
Przesunięcie dopplerowskie ścieżki bezpośredniej można oszacować za pomocą następującego wzoru:
f D , d i r = v m o b λ c cos ϕ cos θ {{displaystyle f_{rm {D,dir}}={frac {v_{rm {mob}}}{{lambda {{rm {c}}}}}cos \phi \i \i \i0}}.

gdzie v m o b {{displaystyle v_{mob}}}

jest prędkością stacji ruchomej, λ c {{displaystyle {lambda _{rm {c}}}

oznacza długość fali nośnej, ϕ {{displaystyle {phi}}

to kąt elewacji satelity, a θ {displaystyle \theta }

to kierunek jazdy w stosunku do satelity.
Dodatkowe przesunięcie dopplerowskie spowodowane poruszaniem się satelity można opisać następująco:
f D , s a t = v r e l , s a t λ c {displaystyle f_{{rm {D,sat}}={frac {v_{rm {rel,sat}}}{{lambda {{rm {c}}}}}

gdzie v r e l , s a t {{displaystyle v_{rm {rel,sat}}}

jest prędkością względną satelity.
AudioEdit
Głośnik Leslie, najczęściej kojarzony i stosowany ze słynnymi organami Hammonda, wykorzystuje efekt Dopplera poprzez użycie silnika elektrycznego do obracania tuby akustycznej wokół głośnika, wysyłając dźwięk po okręgu. Skutkuje to w uchu słuchacza szybko zmieniającymi się częstotliwościami nuty klawiszowej.
Pomiar drgańEdit
Wibrometr laserowy Dopplera (LDV) jest bezkontaktowym przyrządem do pomiaru drgań. Wiązka laserowa z LDV jest kierowana na interesującą nas powierzchnię, a amplituda i częstotliwość drgań są ekstrahowane z Dopplerowskiego przesunięcia częstotliwości wiązki laserowej spowodowanego ruchem powierzchni.
Biologia rozwojowaEdit
Podczas segmentacji zarodków kręgowców, fale ekspresji genów przesuwają się przez mezodermę przedomitową, tkankę, z której powstają prekursory kręgów (somity). Nowy somit powstaje po dotarciu fali do przedniego końca mezodermy presomitycznej. U ryb zebrafish wykazano, że skracanie się mezodermy presomitycznej podczas segmentacji prowadzi do efektu Dopplera, ponieważ przedni koniec tkanki przemieszcza się w kierunku fal. Ten efekt Dopplera przyczynia się do okresu segmentacji.