Jakobian

Algebra > LinearAlgebra > Determinanty >

Kalkulacje i analizy > Calculus > Multivariable Calculus >

Historia i terminologia > Kod Mathematica >

Dając zbiór równań w zmiennych , zapisanych jawnie jako

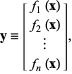(1)

lub bardziej jednoznacznie jako

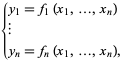${y_1=f_1(x_1,....,x_n); |; y_n=f_n(x_1,...,x_n),$

(2)

Macierz Jakobiana, czasami nazywana po prostu „jakobianem” (Simon i Blume 1994) jest zdefiniowana przez

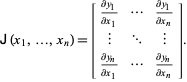(3)

Wyznacznikiem jest wyznacznik jakobianowy (mylnie, często nazywana również „jakobianem”) i oznaczana jest

(4)

Macierz jakobianowa i można obliczyć w języku WolframLanguage za pomocą

 JacobianMatrix := Outer /; Equal @@ (Dimensions /@ {f, x}) JacobianDeterminant := Det] /; Equal @@ (Dimensions /@ {f, x})

Odwzorowanie różniczkowania

(5)

Wskazuje, że jest wyznacznikiem macierzy , a zatem daje stosunki wymiarowych objętości (zawartości) w i ,

(6)

Występuje zatem np. w twierdzeniu o zmianie zmiennych.

Pojęcie jakobianu może być również stosowane do funkcji w więcej niż zmiennych. Na przykład, rozważając i , jakobianów

			(7)
			(8)

można zdefiniować (Kaplan 1984, s. 99).

Dla przypadku zmiennych, jakobian przyjmuje szczególną postać

(9)

gdzie to iloczyn kropkowy, a to iloczyn krzyżowy, co można rozwinąć, aby otrzymać

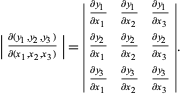(10)