Wibracje
Analiza drgań (VA), stosowana w środowisku przemysłowym lub utrzymaniu ruchu ma na celu zmniejszenie kosztów utrzymania ruchu i przestojów sprzętu poprzez wykrywanie usterek sprzętu. VA jest kluczowym elementem programu monitorowania stanu (CM) i jest często określana jako konserwacja predykcyjna (PdM). Najczęściej VA jest używana do wykrywania usterek w sprzęcie obrotowym (wentylatory, silniki, pompy, przekładnie itp.), takich jak niewyważenie, niewspółosiowość, usterki łożysk tocznych i warunki rezonansowe.
VA może wykorzystywać jednostki przemieszczenia, prędkości i przyspieszenia wyświetlane jako przebieg czasowy (TWF), ale najczęściej używane jest widmo, uzyskane z szybkiej transformaty Fouriera TWF. Widmo drgań dostarcza ważnych informacji o częstotliwości, które mogą wskazać wadliwy element.
Podstawy analizy drgań można zrozumieć poprzez studiowanie prostego modelu masa-sprężyna-tłumik. Rzeczywiście, nawet złożona struktura, taka jak nadwozie samochodu może być modelowana jako „suma” prostych modeli masa-sprężyna-tłumik. Model masa-sprężyna-tłumik jest przykładem prostego oscylatora harmonicznego. Matematyka użyta do opisania jego zachowania jest identyczna z innymi prostymi oscylatorami harmonicznymi, takimi jak obwód RLC.
Uwaga: Ten artykuł nie zawiera matematycznych pochodnych krok po kroku, ale skupia się na głównych równaniach i koncepcjach analizy drgań. Proszę odnieść się do referencji na końcu artykułu w celu uzyskania szczegółowych pochodnych.
Wibracje swobodne bez tłumieniaEdit

Aby rozpocząć badanie amortyzatora masowo-sprężynowego należy założyć, że tłumienie jest pomijalne i że na masę nie działa żadna siła zewnętrzna (i.e. free vibration). Siła przyłożona do masy przez sprężynę jest proporcjonalna do stopnia rozciągnięcia sprężyny „x” (zakładając, że sprężyna jest już ściśnięta z powodu ciężaru masy). Stała proporcjonalności, k, jest sztywnością sprężyny i ma jednostki siły/dystansu (np. lbf/in lub N/m). Ujemny znak oznacza, że siła zawsze przeciwstawia się ruchowi masy do niej przymocowanej:
F s = – k x . {displaystyle F_{s}=-kx.}

Siła generowana przez masę jest proporcjonalna do jej przyspieszenia, co wynika z drugiego prawa ruchu Newtona:
Σ F = m a = m x ¨ = m d 2 x d t 2 . F=ma=m{dot {x}}=m{frac {d^{2}x}{dt^{2}}}}.}

Suma sił działających na masę generuje równanie różniczkowe zwyczajne: m x ¨ + k x = 0. {{displaystyle \ m{ddot {x}}+kx=0.}


Zakładając, że inicjacja drgań rozpoczyna się od rozciągnięcia sprężyny o odległość A i zwolnienia, rozwiązaniem powyższego równania opisującego ruch masy jest:
x ( t ) = A cos ( 2 π f n t ) . {{displaystyle x(t)=A cos(2 π f_{n}t).}

To rozwiązanie mówi, że będzie on oscylował ruchem harmonicznym prostym, który ma amplitudę A i częstotliwość fn. Liczba fn jest nazywana nietłumioną częstotliwością drgań własnych. Dla prostego układu masa-sprężyna, fn jest zdefiniowana jako:
f n = 1 2 π k m . {{displaystyle f_{n}={1 ∑ 2 ∑pi }}{{sqrt {k ∑ m}}.}

Uwaga: częstotliwość kątowa ω (ω=2 π f) z jednostkami radianów na sekundę jest często używana w równaniach, ponieważ upraszcza równania, ale zwykle jest przekształcana na zwykłą częstotliwość (jednostki Hz lub równoważnie cykli na sekundę) przy podawaniu częstotliwości układu. Jeśli znana jest masa i sztywność układu, powyższy wzór pozwala określić częstotliwość, z jaką układ drga po wprowadzeniu go w ruch przez początkowe zaburzenie. Każdy system wibrujący ma jedną lub więcej częstotliwości drgań własnych, przy których wibruje po wystąpieniu zaburzenia. Ta prosta zależność może być użyta do ogólnego zrozumienia, co dzieje się z bardziej złożonym systemem po dodaniu masy lub sztywności. Na przykład, powyższy wzór wyjaśnia, dlaczego, gdy samochód lub ciężarówka jest w pełni załadowany, zawieszenie czuje się „bardziej miękkie” niż bez obciążenia – masa wzrosła, zmniejszając częstotliwość drgań własnych systemu.
Co powoduje, że system wibruje: z punktu widzenia zachowania energiiEdit
Ruch wibracyjny może być rozumiany w kategoriach zachowania energii. W powyższym przykładzie sprężyna została rozciągnięta o wartość x i w związku z tym pewna energia potencjalna ( 1 2 k x 2 {tfrac {1}{2}}kx^{2}}}}

) jest zmagazynowana w sprężynie. Po zwolnieniu sprężyna ma tendencję do powrotu do stanu bez naprężenia (który jest minimalnym stanem energii potencjalnej) i w tym procesie przyspiesza masę. W punkcie, w którym sprężyna osiągnęła stan nierozciągnięcia, cała energia potencjalna, którą dostarczyliśmy rozciągając ją, została przekształcona w energię kinetyczną ( 1 2 m v 2 {tfrac {1}{2}}mv^{2}}}).

). Następnie masa zaczyna zwalniać, ponieważ ściska teraz sprężynę i w procesie tym przekazuje energię kinetyczną z powrotem do potencjalnej. Zatem oscylacja sprężyny jest równoznaczna z przeniesieniem energii kinetycznej z powrotem na energię potencjalną. W tym prostym modelu masa kontynuuje oscylacje w nieskończoność z tą samą wielkością – ale w prawdziwym systemie, tłumienie zawsze rozprasza energię, ostatecznie doprowadzając sprężynę do spoczynku.
Wibracje swobodne z tłumieniemEdit

Gdy do modelu dodamy tłumik „lepki”, wytworzy się siła proporcjonalna do prędkości masy. Tłumienie nazywane jest lepkim, ponieważ modeluje ono wpływ płynu wewnątrz obiektu. Stała proporcjonalności c jest nazywana współczynnikiem tłumienia i ma jednostki Siły w stosunku do prędkości (lbf⋅s/in lub N⋅s/m).
F d = – c v = – c x ˙ = – c d x d t . F_{displaystyle F_{text{d}}=-cv=-c{dot {x}}=-c{frac {dx}{dt}}.}

Sumując siły działające na masę otrzymujemy następujące równanie różniczkowe zwyczajne:
m x ¨ + c x ˙ + k x = 0. {{displaystyle m{text{dot {x}}+c{dot {x}}+kx=0.}.

Rozwiązanie tego równania zależy od wielkości tłumienia. Jeśli tłumienie jest wystarczająco małe, układ nadal drga – ale w końcu, z czasem, przestaje drgać. Ten przypadek nazywany jest niedotłumieniem, co jest ważne w analizie drgań. Jeśli tłumienie jest zwiększone tylko do punktu, w którym system przestaje drgać, system osiągnął punkt krytycznego tłumienia. Jeśli tłumienie zostanie zwiększone powyżej tłumienia krytycznego, układ jest nadmiernie wytłumiony. Wartość, jaką musi osiągnąć współczynnik tłumienia, aby uzyskać tłumienie krytyczne w modelu masa-sprężyna-tłumik wynosi:
c c = 2 km . {{displaystyle c_{text{c}}=2{sqrt {{text{km}}}}.}

Do scharakteryzowania wielkości tłumienia w układzie stosuje się stosunek zwany współczynnikiem tłumienia (znany również jako współczynnik tłumienia i % tłumienia krytycznego). Ten współczynnik tłumienia jest po prostu stosunkiem tłumienia rzeczywistego do ilości tłumienia wymaganego do osiągnięcia tłumienia krytycznego. Wzór na współczynnik tłumienia ( ζ {{displaystyle \zeta }

) modelu masa-sprężyna-tłumik wynosi: ζ = c 2 km . ζ ={c ≥ 2{sqrt {{text{km}}}}.}

Na przykład konstrukcje metalowe (np. kadłuby samolotów, wały korbowe silników) mają współczynniki tłumienia mniejsze niż 0,05, natomiast zawieszenia samochodowe są w zakresie 0,2-0,3. Rozwiązanie układu niedotłumionego dla modelu masa-sprężyna-tłumik jest następujące:
x ( t ) = X e – ζ ω n t cos ( 1 – ζ 2 ω n t – ϕ ) , ω n = 2 π f n . {{displaystyle x(t)=Xe^{-izeta ^{n}t}^cos ^left({sqrt {1-izeta ^{2}}}} ^omega _{n}t- ^phi ^prawo),^qquad ^omega _{n}=2\i f_{n}.}


Wartość X, wielkości początkowej, oraz ϕ , {{displaystyle \\phi ,}

przesunięcia fazowego, zależą od wielkości rozciągnięcia sprężyny. Wzory na te wartości można znaleźć w źródłach.
Tłumione i nietłumione częstotliwości drgań własnychEdit
Głównymi punktami, na które należy zwrócić uwagę w rozwiązaniu są składnik wykładniczy i funkcja cosinus. Termin wykładniczy określa jak szybko system „tłumi” w dół – im większy współczynnik tłumienia, tym szybciej tłumi do zera. Funkcja cosinusowa jest oscylującą częścią rozwiązania, ale częstotliwość oscylacji jest inna niż w przypadku nietłumionym.
Częstotliwość w tym przypadku nazywana jest „tłumioną częstotliwością drgań własnych”, f d , {{displaystyle f_{text{d}},}

i jest związana z nietłumioną częstotliwością drgań własnych następującym wzorem: f d = f n 1 – ζ 2 . {displaystyle f_{text{d}}=f_{n}{sqrt {1-izeta ^{2}}}}.}

Tłumiona częstotliwość drgań własnych jest mniejsza od nietłumionej częstotliwości drgań własnych, ale dla wielu praktycznych przypadków współczynnik tłumienia jest stosunkowo mały i stąd różnica jest pomijalna. Dlatego też, opis tłumiony i nietłumiony jest często pomijany przy podawaniu częstotliwości drgań własnych (np. przy współczynniku tłumienia 0.1, tłumiona częstotliwość drgań własnych jest tylko o 1% mniejsza od nietłumionej).
Plany obok przedstawiają jak współczynniki tłumienia 0.1 i 0.3 wpływają na to jak układ „dzwoni” w dół w czasie. Co jest często wykonywane w praktyce jest eksperymentalnie zmierzyć swobodne wibracje po uderzeniu (na przykład przez młotek), a następnie określić częstotliwość drgań własnych systemu poprzez pomiar szybkości oscylacji, jak również współczynnik tłumienia poprzez pomiar szybkości zanikania. Częstotliwość drgań własnych i współczynnik tłumienia są ważne nie tylko w przypadku drgań swobodnych, ale również charakteryzują sposób zachowania się układu w warunkach drgań wymuszonych.
Wibracje wymuszone z tłumieniemEdit
Zachowanie modelu tłumika masy sprężynowej zmienia się wraz z dodaniem siły harmonicznej. Siła tego typu może być np. generowana przez wirujące niewyważenie.
F = F 0 sin ( 2 π f t ) . {{displaystyle F=F_{0} sin(2 π ft).}

Sumując siły działające na masę otrzymujemy następujące równanie różniczkowe zwyczajne:
m x ¨ + c x ˙ + k x = F 0 sin ( 2 π f t ) . m{displaystyle m{x}}+c{x}}+kx=F_{0} sin(2 π f t).}

Rozwiązanie tego problemu w stanie ustalonym można zapisać jako:
x ( t ) = X sin ( 2 π f t + ϕ ) . {{displaystyle x(t)=Xsin(2 π ft + ϕ ).}

Wynik ten mówi, że masa będzie oscylować z tą samą częstotliwością, f, przyłożonej siły, ale z przesunięciem fazowym ϕ . {{displaystyle \\i0}

Amplituda drgań „X” określona jest następującym wzorem.
X = F 0 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 . X={F_{0} \k}{1 ∑sqrt {(1-r^{2})^{2}+(2 ζ r)^{2}}}}.}

Gdzie „r” jest zdefiniowane jako stosunek częstotliwości harmonicznej siły do nietłumionej częstotliwości drgań własnych modelu masa-sprężyna-tłumik.
r = f f n . r={frac {f}{f_{n}}}}.}

Przesunięcie fazowe, ϕ , {{displaystyle \fi ,}

jest zdefiniowane następującym wzorem. ϕ = arctan ( – 2 ζ r 1 – r 2 ) . ϕ = arctan ∑left({frac {-2zeta r}{1-r^{2}}}} right).}


Wykres tych funkcji, zwany „odpowiedzią częstotliwościową układu”, przedstawia jedną z najważniejszych cech w drganiach wymuszonych. W układzie lekko wytłumionym, gdy częstotliwość wymuszenia zbliża się do częstotliwości drgań własnych ( r ≈ 1 {{displaystyle r}}

) amplituda drgań może stać się ekstremalnie duża. Zjawisko to nazywane jest rezonansem (następnie częstotliwość drgań własnych układu jest często określana jako częstotliwość rezonansowa). W systemach łożyskowania wirników każda prędkość obrotowa, która wzbudza częstotliwość rezonansową jest określana jako prędkość krytyczna.
Jeśli w układzie mechanicznym wystąpi rezonans, może on być bardzo szkodliwy – prowadząc do ostatecznej awarii układu. W związku z tym, jednym z głównych powodów przeprowadzania analizy drgań jest przewidywanie, kiedy ten rodzaj rezonansu może wystąpić, a następnie określenie, jakie kroki należy podjąć, aby zapobiec jego wystąpieniu. Jak widać na wykresie amplitudy, dodanie tłumienia może znacznie zmniejszyć wielkość drgań. Ponadto, wielkość może być zmniejszona, jeśli częstotliwość drgań własnych może być przesunięta z dala od częstotliwości wymuszającej poprzez zmianę sztywności lub masy układu. Jeśli układu nie można zmienić, być może można przesunąć częstotliwość wymuszającą (na przykład zmieniając prędkość maszyny generującej siłę).
Następujące punkty dotyczą drgań wymuszających pokazanych na wykresach odpowiedzi częstotliwościowej.
- Przy danym stosunku częstotliwości, amplituda drgań, X, jest wprost proporcjonalna do amplitudy siły F 0 {{0}}
(np. jeśli podwoimy siłę, drgania podwoją się)
- Przy niewielkim tłumieniu lub jego braku drgania są w fazie z częstotliwością wymuszenia, gdy stosunek częstotliwości r < 1 i o 180 stopni poza fazą, gdy stosunek częstotliwości r > 1
- Gdy r ≪ 1 amplituda jest tylko ugięciem sprężyny pod wpływem siły statycznej F 0 . F_{0}.}
Odchylenie to nazywamy ugięciem statycznym δ s t . {{displaystyle \\delta _{st}.}
Stąd, gdy r ≪ 1 wpływ tłumika i masy jest minimalny.
- Gdy r ≫ 1 amplituda drgań jest w rzeczywistości mniejsza niż ugięcie statyczne δ s t . {{displaystyle ◄delta _{st}.}
W tym rejonie siła generowana przez masę (F = ma) jest dominująca, ponieważ przyspieszenie widziane przez masę rośnie wraz z częstotliwością. Ponieważ ugięcie widziane na sprężynie, X, jest mniejsze w tym obszarze, siła przenoszona przez sprężynę (F = kx) na podstawę jest zmniejszona. W związku z tym, system masa-sprężyna-tłumik izoluje siłę harmoniczną od podstawy montażowej – co określa się mianem wibroizolacji. Większe tłumienie w rzeczywistości zmniejsza efekty wibroizolacji, gdy r ≫ 1, ponieważ siła tłumiąca (F = cv) jest również przenoszona na podstawę.
- bez względu na tłumienie, drgania są 90 stopni poza fazą z częstotliwością wymuszającą, gdy stosunek częstotliwości r = 1, co jest bardzo pomocne, jeśli chodzi o określenie częstotliwości drgań własnych systemu.
- jakiekolwiek jest tłumienie, kiedy r ≫ 1, drgania są o 180 stopni poza fazą z częstotliwością wymuszenia
- jakiekolwiek jest tłumienie, kiedy r ≪ 1, drgania są w fazie z częstotliwością wymuszenia
Przyczyny rezonansuEdit
Resonans jest prosty do zrozumienia, jeśli sprężyna i masa są postrzegane jako elementy magazynujące energię – z masą magazynującą energię kinetyczną i sprężyną magazynującą energię potencjalną. Jak już wcześniej wspomniano, gdy na masę i sprężynę nie działa żadna siła zewnętrzna, przekazują one energię tam i z powrotem z prędkością równą częstotliwości drgań własnych. Innymi słowy, aby efektywnie pompować energię zarówno do masy jak i do sprężyny, źródło energii musi dostarczać ją z prędkością równą częstotliwości naturalnej. Przyłożenie siły do masy i sprężyny jest podobne do pchania dziecka na huśtawce, pchnięcie jest potrzebne w odpowiednim momencie, aby huśtawka wznosiła się coraz wyżej. Podobnie jak w przypadku huśtawki, przyłożona siła nie musi być duża, aby uzyskać duże ruchy, ale musi po prostu dodać energii do układu.
Tłumik, zamiast magazynować energię, rozprasza ją. Ponieważ siła tłumienia jest proporcjonalna do prędkości, im większy ruch, tym bardziej tłumik rozprasza energię. Dlatego istnieje punkt, w którym energia rozpraszana przez tłumik równa się energii dodanej przez siłę. W tym momencie układ osiągnął swoją maksymalną amplitudę i będzie kontynuował drgania na tym poziomie tak długo, jak długo przyłożona siła pozostanie niezmieniona. Jeśli nie ma tłumienia, nie ma nic, co mogłoby rozproszyć energię i, teoretycznie, ruch będzie rósł w nieskończoność.
Zastosowanie „złożonych” sił w modelu masa-sprężyna-tłumikEdit
W poprzednim rozdziale do modelu została zastosowana tylko prosta siła harmoniczna, ale można to znacznie rozszerzyć używając dwóch potężnych narzędzi matematycznych. Pierwszym z nich jest transformata Fouriera, która wykorzystuje sygnał jako funkcję czasu (dziedzina czasu) i rozkłada go na jego składowe harmoniczne jako funkcję częstotliwości (dziedzina częstotliwości). Przykładowo, przykładając do modelu masa-sprężyna-tłumik siłę, która powtarza się w następującym cyklu – siła równa 1 niuton przez 0,5 sekundy, a następnie brak siły przez 0,5 sekundy. Ten rodzaj siły ma kształt fali kwadratowej o częstotliwości 1 Hz.
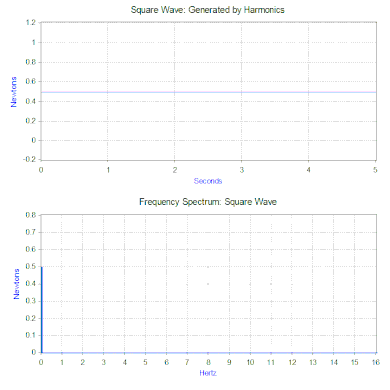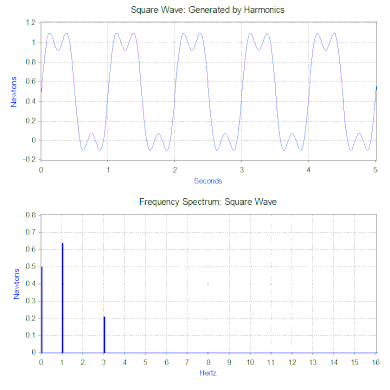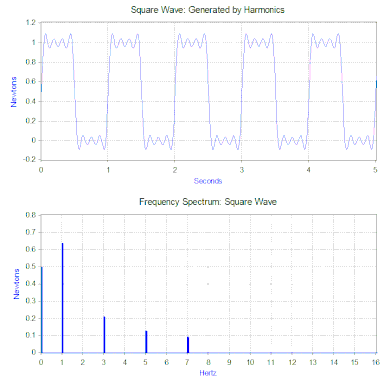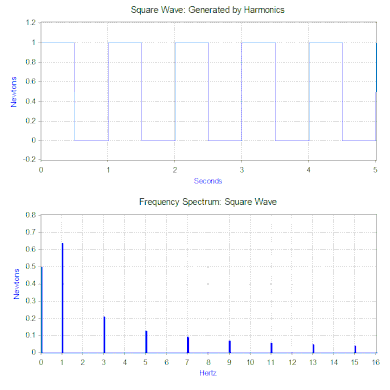
Przekształcenie Fouriera fali kwadratowej generuje widmo częstotliwości, które przedstawia wielkość harmonicznych, które tworzą falę kwadratową (faza jest również generowana, ale zazwyczaj ma mniejsze znaczenie i dlatego często nie jest wykreślana). Transformata Fouriera może być również używana do analizy funkcji nieokresowych, takich jak stany nieustalone (np. impulsy) i funkcje losowe. Transformata Fouriera jest prawie zawsze obliczana przy użyciu algorytmu komputerowego szybkiej transformaty Fouriera (FFT) w połączeniu z funkcją okna.
W przypadku naszej kwadratowej fali siły, pierwsza składowa jest w rzeczywistości stałą siłą 0,5 niutona i jest reprezentowana przez wartość przy 0 Hz w widmie częstotliwości. Następną składową jest sinusoida o częstotliwości 1 Hz i amplitudzie 0,64. Jest ona przedstawiona linią o częstotliwości 1 Hz. Pozostałe składowe mają nieparzyste częstotliwości i potrzeba nieskończonej ilości sinusów, aby wygenerować idealną falę kwadratową. Stąd, transformata Fouriera pozwala interpretować siłę jako sumę sił sinusoidalnych, zamiast bardziej „złożonej” siły (np. fali kwadratowej).
W poprzednim rozdziale, rozwiązanie drgań było podane dla pojedynczej siły harmonicznej, ale transformata Fouriera w ogólności daje wiele sił harmonicznych. Drugie narzędzie matematyczne, „zasada superpozycji”, pozwala na sumowanie rozwiązań pochodzących od wielu sił, jeśli układ jest liniowy. W przypadku modelu sprężyna-masa-tłumik, układ jest liniowy, jeśli siła sprężyny jest proporcjonalna do przemieszczenia, a tłumienie jest proporcjonalne do prędkości w interesującym nas zakresie ruchu. Stąd, rozwiązaniem problemu z falą kwadratową jest zsumowanie przewidywanych drgań z każdej z sił harmonicznych znalezionych w widmie częstotliwości fali kwadratowej.
Model odpowiedzi częstotliwościowejEdit
Rozwiązanie problemu drgań może być postrzegane jako relacja wejście/wyjście – gdzie siła jest wejściem, a wyjściem są drgania. Przedstawienie siły i drgań w dziedzinie częstotliwości (magnitudy i fazy) pozwala na uzyskanie następującej zależności:
X ( i ω ) = H ( i ω ) ⋅ F ( i ω ) lub H ( i ω ) = X ( i ω ) F ( i ω ) . {{displaystyle X(i ω )=H(i ω )⋅ F(i ω ){{text{ lub }}H(i ω )={X(i ω )⋅ F(i ω )}.

H ( i ω ) {{displaystyle H(iomega )}

nazywana jest funkcją odpowiedzi częstotliwościowej (zwana również funkcją przenoszenia, ale nie jest technicznie tak dokładna) i posiada zarówno składową magnitudową, jak i fazową (jeśli jest reprezentowana jako liczba złożona, składową rzeczywistą i urojoną). Wielkość funkcji odpowiedzi częstotliwościowej (FRF) została przedstawiona wcześniej dla układu masa-sprężyna-tłumik. | H ( i ω ) | = | X ( i ω ) F ( i ω ) | = 1 k 1 ( 1 – r 2 ) 2 + ( 2 ζ r ) 2 , gdzie r = f f n = ω ω n . W związku z tym, że nie jest to możliwe, nie można powiedzieć, że nie jest to możliwe,text}} gdzie }r={frac {f}{f_{n}}}={frac {omega }{omega _{n}}}.}

Fazę FRF przedstawiono również wcześniej jako:
∠ H ( i ω ) = – arctan ( 2 ζ r 1 – r 2 ) . ∠ ∠angle H(i ω )= – arctan ∠left({frac {2 ζ r}{1-r^{2}}}}right).}


Na przykład obliczenie FRF dla układu masa-sprężyna-tłumik o masie 1 kg, sztywności sprężyny 1.93 N/mm i współczynniku tłumienia 0,1. Wartości sprężyny i masy dają częstotliwość drgań własnych 7 Hz dla tego konkretnego układu. Zastosowanie wcześniejszej fali kwadratowej o częstotliwości 1 Hz pozwala na obliczenie przewidywanych drgań masy. Rysunek ilustruje otrzymane drgania. Tak się składa, że w tym przykładzie czwarta harmoniczna fali kwadratowej przypada na 7 Hz. Odpowiedź częstotliwościowa amortyzatora masowo-sprężynowego daje zatem wysoki poziom drgań 7 Hz, mimo że siła wejściowa miała stosunkowo niską harmoniczną 7 Hz. Ten przykład podkreśla, że wynikowe drgania zależą zarówno od funkcji wymuszającej, jak i od układu, do którego przyłożona jest siła.
Na rysunku pokazano również reprezentację w dziedzinie czasu wynikowych drgań. Odbywa się to poprzez wykonanie odwróconej transformaty Fouriera, która przekształca dane w dziedzinie częstotliwości na dane w dziedzinie czasu. W praktyce rzadko się to robi, ponieważ widmo częstotliwości dostarcza wszystkich niezbędnych informacji.
Funkcja odpowiedzi częstotliwościowej (FRF) niekoniecznie musi być obliczana na podstawie wiedzy o masie, tłumieniu i sztywności układu – ale może być mierzona eksperymentalnie. Na przykład, jeśli znana siła w zakresie częstotliwości jest stosowana, a jeśli związane z tym wibracje są mierzone, funkcja odpowiedzi częstotliwościowej może być obliczona, charakteryzując w ten sposób system. Technika ta jest stosowana w dziedzinie eksperymentalnej analizy modalnej w celu określenia charakterystyki drgań konstrukcji.


