O Que Significa o Factor de Poder?

Baixo factor de potência reduz a capacidade de distribuição de um sistema eléctrico ao aumentar o fluxo de corrente. Portanto, ter um factor de potência baixo é ineficiente e dispendioso. Mas o que é factor de potência e o que o afecta?

Um sistema de distribuição típico é limitado na quantidade de corrente que pode transportar; o factor de potência, expresso em percentagem, é um indicador da quantidade de corrente total que pode ser utilizada para criar trabalho (potência activa). Quanto mais próximo o factor de potência estiver de 1,00 (100%), menor a quantidade de corrente necessária para realizar o referido trabalho.

Por exemplo, uma carga com um factor de potência de 0,80 significa que apenas 80% da potência está a ser utilizada eficazmente para realizar trabalho. Num mundo perfeito, toda a energia retirada do sistema de energia seria convertida em trabalho útil, mas isto não é assim no mundo real. Para descrever completamente o factor de potência, são necessárias equações complexas. Para uma compreensão mais simples, porém, o Departamento de Energia dos EUA utiliza uma analogia simples da potência necessária para um cavalo puxar um carrinho por um trilho.

Idealmente, o cavalo seria colocado em frente do vagão para fornecer a força de reboque mais eficiente; contudo, isso nem sempre é possível. O ângulo do reboque representa a alteração do factor de potência – quanto menor o ângulo, melhor o factor de potência, quanto maior o ângulo, menor o factor de potência (Figura 1).

>p>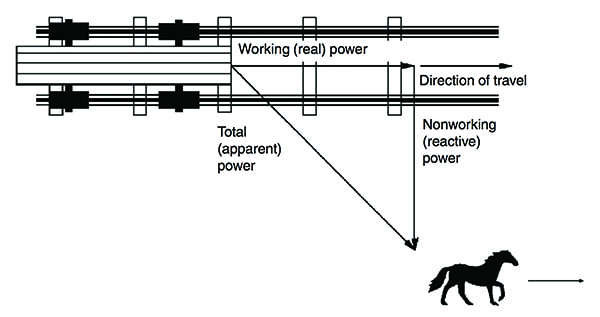br>

1. Os ângulos afectam o trabalho útil. A analogia aqui mostrada proporciona uma visualização para ajudar a compreender o factor de potência. O factor de potência é definido como a relação entre a potência real (de trabalho) e a potência aparente (total). Se o cavalo for conduzido mais próximo do centro da pista, o ângulo de tracção lateral diminui, e a potência real aproxima-se do valor da potência aparente. Fonte: U.S. Department of Energy

br>>p> A energia total necessária para puxar o vagão é a potência aparente. A energia real que move o vagão é a potência real. A energia não utilizada a partir do ângulo de tracção do cavalo é a potência reactiva. Por outras palavras, a potência real, também referida como potência de trabalho (kW), executa o trabalho real de movimento, calor e luz. A potência reactiva, ou potência não funcional (kVar), sustenta o campo magnético de uma carga reactiva (geralmente indutiva). A corrente utilizada para criar a energia reactiva não é utilizada para criar trabalho; contudo, esta corrente coloca uma carga sobre o sistema de distribuição, o fornecedor de electricidade, e a factura eléctrica de uma instalação.

A soma vectorial da potência de trabalho e da potência não de trabalho é a potência total (potência aparente):

P>Potência aparente = √ (potência real2 + potência reactiva2)

que é utilizada para calcular o factor de potência:

Factor de potência = Potência real / Potência aparente = cosseno do ângulo (ϕ)

Fundamentos de tensão e corrente

Para compreender o factor de potência, devemos primeiro compreender alguma teoria básica de corrente alternada (CA) e as formas de onda a ela associadas. A tensão num sistema CA alterna entre positiva e negativa (numa forma sinusoidal) e força a corrente a comportar-se de forma semelhante. Isto ocorre 60 vezes por segundo (num sistema de 60-Hz), variando de 0 a 360 graus. Ao contrário dos sistemas CA, a tensão num sistema de corrente contínua constante (CC) não muda.

Porque o valor instantâneo da tensão CA está continuamente a mudar, a ciência definiu uma medida diferente para as quantidades CA, nomeadamente o valor RMS (root mean square). O valor RMS de uma forma de onda AC produz o mesmo efeito de aquecimento que uma forma de onda DC do mesmo valor.

O RMS é a raiz quadrada da média aritmética dos quadrados de um conjunto de valores instantâneos ao longo de um período (ciclo). Quando a tensão e corrente são puramente sinusoidais, a tensão e corrente RMS pode ser encontrada a partir da tensão e corrente de pico (pk):

VRMS = Vpk / √2

119.5 VRMS = 169 Vpk / 1.414

Similiarmente,

IRMS = Ipk / √2

75 ARMS = 106 Apk / 1.414

P>P>P>Pode estar a perguntar-se, o que é que isto tem a ver com o factor de potência? Os cálculos de potência para CA requerem o conhecimento da tensão RMS, corrente RMS, e a relação de fase sinusoidal. Assim, para resumir, RMS é uma medida do efeito de aquecimento, calculado a partir de uma forma de onda, que permite a comparação da CA com a CC. Qualquer mudança de fase de uma forma de onda sinusoidal pura indica o factor de potência.

O que se segue é uma comparação de como o factor de potência afecta o kVA de saída em duas cargas monofásicas diferentes.

Para um aquecedor eléctrico de 9-kW (120 VAC, 75 A) com factor de potência de entrada 1,0 (PF):

p>P = √1ϕ x 120 VAC x 75 A x 1,0 PF = 9 kW

kVA = √1ϕ x 120 VAC x 75 A = 9 kVA

Para um carregador de bateria de 9-kW (120 VAC, 75 A) com 0.866 entrada PF:

p>P = √1ϕ x 120 VAC x 86,6 A x 0,866 PF = 9 kW

kVA = √1ϕ x 120 VAC x 86,6 A = 10,392 kVA

P>Embora cada carga consuma 9 kW de potência, o factor de potência de entrada do carregador de bateria é de 0,866. O factor de potência mais baixo requer um adicional de 11,6 A para funcionar, que eventualmente é fornecido pela companhia de electricidade. Não só a corrente reactiva adicional deve ser comprada, mas também o tamanho do sistema de distribuição deve ser aumentado para lidar com a corrente adicional.

Que afecta o factor de potência?

Factor de potência refere-se à relação entre a potência activa (potência útil) e a potência aparente (total). Esta relação é uma medida de quão eficazmente a electricidade está a ser utilizada.

Carga Resistiva Linear. Num sistema CA, as cargas são categorizadas pela forma como extraem a corrente. Uma carga resistiva linear é uma carga puramente resistiva, sem componentes indutivos nem capacitivos, tais como aquecedores de espaço eléctricos e iluminação incandescente. As curvas de tensão e corrente intersectam a coordenada zero no mesmo ponto.

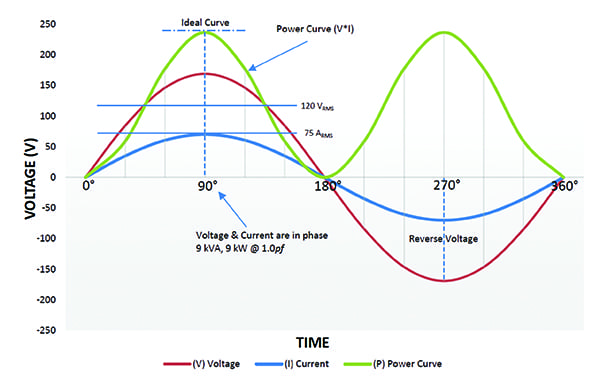
A curva de potência (P) na Figura 2 é calculada pela tensão (V) e corrente (I), mostrada como a área positiva do gráfico. Neste exemplo, a tensão e a corrente são 120 VRMS e 75 ARMS, respectivamente. O produto dos dois é 9 kVA ou 9 kW. A tensão e a corrente estão “em fase”, e 100% da potência (potência de trabalho) está a ser utilizada eficazmente para fazer trabalho útil. O factor de potência para este tipo de carga é 1.0.

br>

br>

2. Cargas resistivas lineares. Tensão e corrente estão em fase com factor de potência igual a 1,0 para cargas puramente resistivas. Cortesia: Controlos de estado sólido Ametek

br> Cargas não resistivas/Reactivas lineares. É invulgar encontrar cargas puramente resistivas; a maioria das cargas tem um componente reactivo adicional. Estas cargas não resistivas/reativas constituem uma grande percentagem de todas as cargas. A forma de onda de corrente é desviada da forma de onda de tensão de modo a ficar “fora de fase”. Se a carga é indutiva, a corrente atrasa a tensão; se a carga é capacitiva, a corrente conduz.

As instalações industriais tendem a ter cargas com factor de potência retardado (cargas indutivas). Estes tipos de cargas podem ser motores de indução, estrangulamentos, e transformadores. As cargas de factor de potência líder (cargas capacitivas) são menos comuns e são geralmente cabos subterrâneos ou certas fontes de alimentação de modo de interruptor.

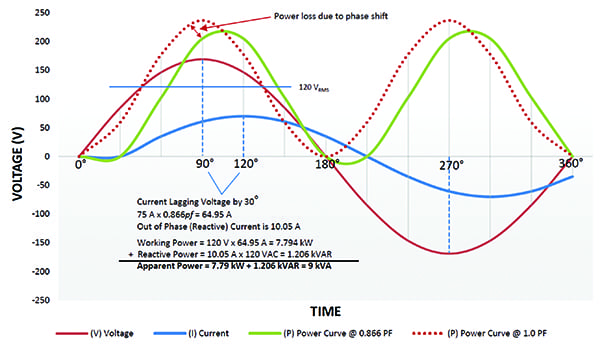
Na Figura 3, a mesma carga da Figura 2 tem agora a forma de onda de tensão e corrente fora de fase em 30 graus. Como se trata de uma forma de onda indutiva, a corrente está agora atrasada.

br>

3. Cargas indutivas. Tensão e corrente estão fora de fase para cargas lineares não-resistivas/reactivas. Neste exemplo de carga indutiva, a corrente atrasa a tensão em 30 graus com factor de potência de 0,866. Cortesia: Ametek Controlos de estado sólido

br>>p>Carga não linear – Harmónica. Os actuais ambientes industriais não só têm cargas resistivas, indutivas e capacitivas, mas muitos também incluem equipamento baseado no estado sólido, tais como fontes de alimentação de comutação, unidades de CC, unidades de frequência variável (VFD), balastros electrónicos, soldadores de arco, e fornos com temperatura controlada. Estas são todas cargas não lineares, ou cargas para as quais a corrente não é sinusoidal, mesmo quando a tensão é sinusoidal. A natureza não-inusoidal destas formas de onda é expressa usando harmónicas.

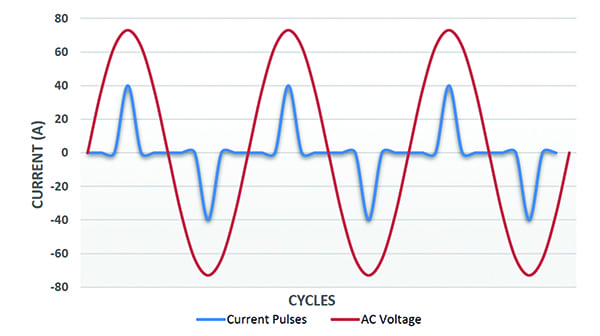
Harmónicas são formas de onda de amplitude variável a frequências que são múltiplos da frequência fundamental da tensão (50 Hz ou 60 Hz). São sobrepostas à forma de onda sinusoidal da corrente para criar a forma de onda da corrente total. A figura 4 é um exemplo de tal forma de onda de corrente.

br>

br>

4. Cargas não lineares. Este gráfico mostra as formas de onda de tensão e corrente de uma fonte de alimentação não linear com harmónicos. É mostrado sem uma mudança de fase de corrente de 30 graus para maior clareza. Cortesia: Ametek Controlos de estado sólido

br>>p> O valor RMS de toda a corrente é encontrado através da soma do valor RMS de cada corrente harmónica. Dada uma forma de onda de 60-Hz, isto significa que uma segunda frequência harmónica seria 120 Hz (60 Hz x 2 = 120 Hz) e as 3ª, 4ª e 5ª frequências harmónicas seriam 180 Hz, 240 Hz, e 300 Hz, respectivamente. Como múltiplos da frequência fundamental, os harmónicos podem ser expressos como 2f, 3f, 4f, etc.

A distorção harmónica total da corrente (THD) é a soma de todos os componentes harmónicos da forma de onda actual comparados com o componente fundamental da onda actual. Como se mostra abaixo, é uma razão entre o valor RMS dos harmónicos da corrente e o valor RMS da corrente fundamental.

ITHD = RMS dos harmónicos da corrente / RMS da corrente fundamental = √(I22 + I32 + I42 + …) / I1 x 100%

Para formas de onda puramente sinusoidais, a mudança de fase entre tensão e corrente é suficiente para quantificar o factor de potência (PF). Para as formas de onda que não são sinusoidais, o termo factor de potência de deslocamento (DpPF) é utilizado para quantificar o deslocamento de fase entre os fundamentos das duas formas de onda (os componentes 50-Hz ou 60-Hz). Para as mesmas formas de onda não sinusoidais, é definido um termo para quantificar o efeito das harmónicas sobre o PF. Este termo é denominado factor de potência de distorção (DF).

DF = 1 / √(1 + THD2)

Para encontrar o factor de potência total (PFT), utiliza-se a seguinte equação:

PFT = DF x DpPF

Correlações do Factor de Potência

Para cargas lineares, o triângulo de potência é um triângulo direito que mostra as relações entre potência funcional, reactiva, e aparente. A relação entre o trabalho e a potência aparente é PF. O valor pode variar entre 0,0 e 1,0,

Potência de trabalho, também chamada potência verdadeira, potência real, ou potência activa, executa o trabalho real de movimento/aquecimento/luz, etc. e é medida em watts (W). A potência reactiva sustenta o campo magnético ou eléctrico em dispositivos, tais como bobinas solenóides, enrolamentos de motores, enrolamentos de transformadores, condensadores, e balastros, sem fazer o trabalho real. Esta energia extra é medida em volt-amperes reactivos (VAR) e é por vezes chamada de energia “sem watts”. A potência aparente combina potência de trabalho e potência reactiva, e é medida em volt-amperes (VA).

p>O ângulo de fase (ϕ) em graus, representa a “ineficiência” da carga e corresponde à impedância reactiva total (Z) ao fluxo de corrente na carga. Quanto maior for o ângulo de fase, maior será a potência reactiva. As cargas não lineares adicionam um elemento extra à potência total (aparente) sem adicionar à potência activa, diminuindo ainda mais o factor de potência. ■

-David McKinnon é engenheiro de aplicações sénior da Ametek Solidstate Controls. Agradecimentos especiais a Bogdan Proca, PhD e Doug King pelas suas contribuições.