Qual é a diferença entre PNP e NPN?

Este artigo apareceu em Microondas & RF e foi publicado aqui com permissão.

O que vai aprender:

• A máxima produção de um canal em função da taxa de símbolo e largura de banda.
• A máxima produção de um canal em função da interferência de ruído.
• Como as considerações de produção vão até ao utilizador.

É muito fácil e normal concentrar-se nas características principais dos principais componentes de um sistema de comunicações ou ligação, e considerar outros itens e questões como periféricos e não tão importantes. O facto de ter acontecido uma quantidade surpreendente com as ligações de comunicações via satélite, especialmente as ligações móveis remotas, é a razão para esta missiva.

Aqui está uma situação hipotética. É um soldado. Está implantado numa zona montanhosa do Médio Oriente, transportando um terminal de satélite Intelsat mais antigo para acesso imediato ao quartel-general, e o quartel-general alugou um transponder de 72-MHz para seu uso exclusivo.

Um lugar agradável e seguro para estar é numa caverna, por isso, enfia um cabo de comunicações no terminal de satélite à entrada da caverna e recosta-se para verificar com o seu posto de trabalho que está ligado ao terminal com um modem de chaveamento em quadratura (QPSK). O check-in é óptimo, mas a comunicação é péssima. A empresa de satélite garante-lhe 72 Mb/s (1 bit por Hz), mas mal recebe menos de 35 Mb/s. Deveria ter arranjado um terminal mais recente? Deveria estar a utilizar outro sistema?

Nyquist Maximum Data Rates

A resposta real é o que Harry Nyquist e Claude Shannon disseram sobre as taxas máximas de dados em todos os canais, incluindo aquele cabo de comunicações. Harry Nyquist observou, como foi exaustivamente documentado1, o número máximo de bits que se pode obter através de um canal (ruído não considerado) é:

Max R = 2 H Log2V

onde H é a largura de banda do canal e V é o número de símbolos discretos (chaveamento binário de mudança de fase, ou BPSK, é 2, QPSK é 4, etc.).

se não estiver familiarizado com log2, não é difícil uma vez que se habitue a ele. O log2V é simplesmente o expoente ao qual 2 deve ser elevado para igual V. Assim, se V é BPSK (2), então a expressão log2V é simplesmente 1, visto que 21 é na realidade 2; e se V é QPSK (4), então a expressão log2V é 2 visto que 22 é na realidade 4, e assim por diante.

Se estiver a utilizar um cabo Cat 3 de 10 MHz, então a taxa máxima de dados INTO do terminal de satélite é BPSK 20 Mb/s, QPSK 40 Mb/s, e 8PSK 30 Mb/s, em função das relações log2. A figura 1 mostra o número de estados e o seu log para o equivalente à base 2. Portanto, o limite Nyquist, utilizando o modem QPSK, é de 40 Mb/s.

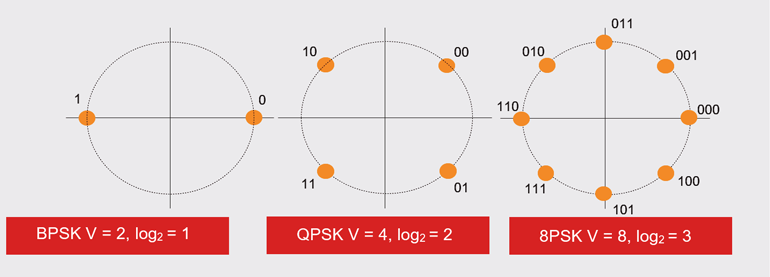1. BPSK, com dois estados, tem um valor log2 de 1; QPSK, com quatro estados, tem um valor log2 de 2; e assim por diante.

Shannon Maximum Data Rates

Well, Harry Nyquist estava a trabalhar na questão das taxas máximas de dados sem considerar o ruído enquanto Claude Shannon o estava a trabalhar estritamente em função do ruído. A sua equação2 diz:

Max R = H log2 (1 + SNR)

onde H é novamente a largura de banda do canal e o SNR é a potência do sinal dividida pela potência do ruído, geralmente dada em dB. Vamos assumir que o SNR nesse mesmo cabo Cat 3 é cerca de 30 dB ou 1.000 em números brutos (o SNR deve ser reconvertido para o seu valor racional para calcular um exponencial). Uma vez que temos vindo a aumentar a escala de exponenciais de 2, podemos continuar a fazer isso. A figura 2 mostra essa progressão.

2. Um número, mostrado na linha superior, tem um valor exponencial, mostrado na linha inferior, e demonstra o significado da temperatura sonora do sistema no que diz respeito a uma taxa de passagem de canal.

Se arredondarmos um pouco por simplicidade, 1.001 está mais próximo de 1.024 do que qualquer outro incremento e 2 elevado para a 10ª potência dá um valor muito mais próximo do que qualquer outro expoente. Sentado na sua caverna com um cabo Cat 3 de 10 MHz de largura de banda, Claude Shannon diz que deve obter uma taxa de dados de 10 x 106 (10) = 100 Mb/s.

Se Claude Shannon diz que pode obter uma taxa máxima de dados no terminal de comunicações via satélite de 100 Mb/s e Harry Nyquist diz que só pode obter 40 Mb/s de e para a sua estação de trabalho equipada com QPSK, quem está certo?

Vejamos outra analogia. A Universidade de Notre Dame tem uma equipa de futebol academicamente constrangida mas relativamente boa. Por outro lado, tem uma grande banda de marcha porque os músicos excelentes são frequentemente excelentes estudantes do ensino secundário. Para entrar em campo, a banda tem de marchar através de dois arcos, um que permite 15 membros em marcha e outro que permite 10. Como é que os membros se aproximam da banda? Bem, da mesma forma, Nyquist e Shannon não estão a competir. São apenas dois portões diferentes com duas restrições diferentes.

Não é apenas o sistema principal. É o go-intas e o go-outas até às mãos, digitando no teclado. E os artigos originais publicados pelo físico Nyquist3 e pelo matemático/engenheiro Shannon4 ainda têm algo a dizer-nos.

1. Um exemplo da equação pode ser encontrado em qualquer edição de Data and Computer Communications de William Stallings listada sob Nyquist Bandwidth. Nota: Autores diferentes usam letras diferentes para designar taxa de dados, largura de banda, etc.

2. Tal como com Nyquist a equação que se encontra em qualquer edição de Data and Computer Communications de William Stallings, esta está listada em Shannon Capacity Formula. Nota: Diferentes autores usam letras diferentes para designar taxa de dados, largura de banda, etc.

3. Certos tópicos na teoria da transmissão telegráfica (que implicava o limite) foram apresentados na Convenção de Inverno da AIEE, Nova Iorque, N.Y., 13-17 de Fevereiro de 1928. Foi republicado como “Classic Paper” nas Actas do IEEE em Fevereiro de 2002.

4. “Communications in the Presence of Noise” foi publicado nas Actas do IRE em Janeiro de 1949, nove anos após ter sido escrito.