Quão Precisas São as Fórmulas para a Lacuna Osmolal?

A lacuna osmolal é mais comummente usada no rastreio de ingestão de álcool tóxico. Na ausência de outros solutos não medidos, o sódio, a glucose e a ureia são os solutos primários responsáveis pela osmolalidade. Se estiver presente uma diferença significativa (geralmente o corte é > 10) entre a osmolalidade medida directamente e a osmolalidade calculada (Sosm), então a diferença (a fenda osmolal) pode representar a presença de um soluto não medido.

O conceito da fenda osmolal do soro tem sido sempre difícil de apreender e ainda mais difícil de explicar. Como o sódio é o principal cátion extracelular, faz sentido que o sódio (e o ânion correspondente, seja cloreto ou bicarbonato) constitua a parte de leão da osmolalidade. Mas e outros catiões como o cálcio, potássio, ou magnésio? Não contam de todo? Para tornar as coisas mais confusas, alguns países (como os EUA) reportam em mEq/L (ou mmol/L) mas reportam BUN e glucose em mg/dL.

P>P>Fórmula mais básica:

p>Fórmula Sosm calculada = (2 x Na) + (Glu/18) + (BUN/2.8)

Na é multiplicada por 2 para ter em conta o seu anião correspondente. A glucose e o BUN precisam de ser divididos por factores para contabilizar os seus pesos moleculares correspondentes (180 e 28, respectivamente) para converter o mg/dL em mosm/L.

Agora, vamos usar alguns números reais num exemplo fictício: O paciente A foi encontrado inconsciente em casa perto de garrafas não marcadas. Na 138 mEq/L, BUN 28 mg/dL, Cr 1,4 mg/dL, Glu 90 mg/dL, medida Sosm 315 mosm/kg

Fórmula Sosm calculada = (2 x Na) + (Glu/18) + (BUN/2,8)

Sosm calculada = (2 x 138) + (90/18) + (28/2).8) = 291

Fenda osmolal = Sosm medido – Sosm calculado

Fenda osmolal = 315 – 291 = 24

A presença de uma fenda osmolal elevada (> 10) neste cenário aumenta o ritmo cardíaco de qualquer nefrologista, mas não esqueçamos que a ingestão de etanol também pode contribuir para a fenda osmolal. Vamos assumir que este paciente bebeu vodka em excesso e teve um nível de etanol medido de 92 mg/dL. O factor de correcção a converter para mmol/L com base no peso molecular do etanol é 4,6,

Sosm calculado (contabilizado para EtOH) = (2 x 138) + (90/18) + (28/2,8) + (92/4).6) = 311

Fasso de osmolal = 315 – 311 = 4

Se for a uma calculadora online comum como a MDCalc, a sua fórmula é a mesma que demonstrámos acima.

Até agora tudo bem, mas vários problemas surgem. Esta não é de modo algum a única equação utilizada para calcular Sosm – ver tabela abaixo:

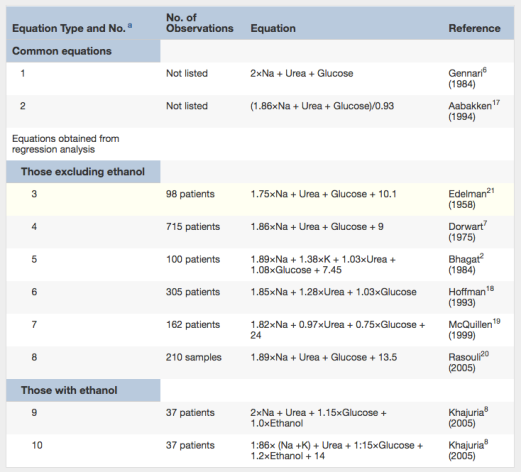
Equações para o Cálculo da Osmolaridade anteriormente publicadas. Nota: Todos os valores estão em mmol/L. Para uso com unidades convencionais, multiplicar ureia por 2,8, glucose por 18, e etanol por 4,6. Tabela 1 de Lepeytre et al, AJKD © National Kidney Foundation.

Adicionalmente, várias destas fórmulas foram realizadas em pequenas coortes sem validação externa, e as medições foram feitas com equipamento desactualizado.

Num artigo recente da AJKD, Lepeytre et al relataram as suas conclusões sobre o desenvolvimento de uma equação mais precisa para calcular a diferença osmolal num grande coorte utilizando equipamento automatizado moderno, e compararam esta nova equação com fórmulas previamente publicadas utilizando métodos estatísticos vigorosos. Esta coorte começou com mais de 9.000 medições onde a osmolalidade do soro, sódio, potássio, ureia, glucose, e etanol foram obtidos simultaneamente. Foram excluídos os doentes com valores aberrantes e dados em falta subsequentes, deixando aproximadamente 7.500 amostras que foram analisadas.

Fechar a metade tinham um nível de etanol detectável. Os autores realizaram modelos de regressão linear sobre esta coorte e analisaram de forma semelhante fórmulas previamente publicadas. A adição de potássio não modificou significativamente o cálculo da diferença osmolal, pelo que foi excluída por simplicidade. Identificaram então que coeficientes de 1,2 para a ureia, 1,4 para a glucose, e 1,2 para o etanol gerariam a medida mais precisa e precisa, o que levou à seguinte fórmula:

(2 x Na) + (1,2 x Ureia) + (1,4 x Glucose) + (1.2 x EtOH) ← todas as unidades em mmol/L

ou para converter isto em unidades convencionais onde BUN, Glucose, e EtOH estão em mg/dL:

(2 x Na) + (1,2 x BUN / 2,8) + (1,4 x Glucose / 18) + (1,2 x EtOH / 4,6)

Existiram 138 medições na coorte com ingestão de álcool tóxico. Lepeytre et al avaliaram como esta nova fórmula funcionava estatisticamente quando comparada com outras fórmulas na previsão de qual destes pacientes necessitaria de um tratamento específico, como o fomepizol ou a diálise. Utilizando os coeficientes acima indicados para a ureia, glicose e etanol, a equação modificada foi claramente superior às fórmulas anteriormente publicadas. Usando um corte de um intervalo osmolal > 5,0 levou a um PPV de 50% e 99% NPV, e usando um intervalo osmolal de > 10,0 levou a 82% PPV e 96% NPV na identificação de pacientes com ingestão de álcool tóxico.

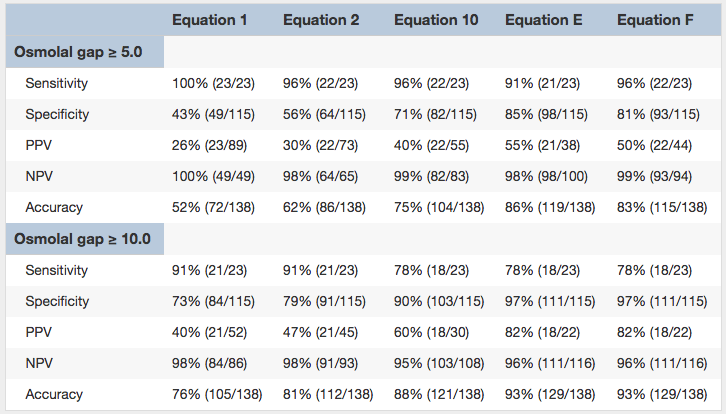
Sensibilidade, Especificidade, e Valores Predictivos Positivos e Negativos das Equações 1, 2, 10, E, e F para Presença de Álcoois Tóxicos ≥ 5 mmol/L, por Osmolal Gap. Os valores são dados em percentagem (n/N). As equações são etiquetadas com números para identificar equações previamente publicadas (1, 2, 10) e letras para identificar novas equações (E, F). Tabela 5 de Lepeytre et al, AJKD © National Kidney Foundation.

O que devemos fazer com isto? Lepeytre et al notam que a fórmula comum que utilizámos para o Paciente A acima criou um elevado número de casos falso-positivos para álcoois tóxicos. A fórmula assume que a ureia, glicose e etanol se comportam como solutos ideais, semelhantes ao Na. Este artigo (e publicações anteriores) sugere que isto pode não ser verdade; portanto, a necessidade de um coeficiente de modificação.

Quais são as potenciais implicações clínicas da vida real? Por exemplo, uma taxa mais baixa de falsos positivos traduzir-se-ia em menos doses empíricas de fomepizol (ou mesmo diálise) em pacientes suspeitos de ingestão de álcool tóxico. Os autores também sublinham que a presença de um intervalo osmolal elevado não significa a ingestão de álcool tóxico se o contexto clínico não se enquadrar. Como na maioria das coisas em medicina, o historial de exposição é mais importante do que o cálculo para determinar a probabilidade de ingestão de álcool tóxico.

Este artigo representa a maior coorte de lacunas osmolares alguma vez estudada, e a equação derivada subsequentemente supera as anteriormente publicadas. Com validação externa, podemos ver esta nova fórmula em calculadoras online num futuro próximo.

– Post preparado por Timothy Yau, Editor de Meios Sociais da AJKD. Siga-o @Maximal_Change.

Para ver o resumo do artigo Lepeytre et al ou o texto completo (assinatura requerida), visite AJKD.org.

Title: Fórmulas de Osmolaridade Calculada e Osmolal Gap: A Study of Diagnostic Accuracy
Authors: F. Lepeytre, M. Ghannoum, H. Ammann, F. Madore, S. Troyanov, R. Goupil, e J. Bouchard
DOI: 10.1053/j.ajkd.2017.03.023