Ujemny eksperyment dwumianowy / dystrybucja: Definicja, Przykłady

Twierdzenie dwumianu > Eksperyment z ujemnym dwumianem

Zdjęcie: UCSF

Doświadczenie dwumianu ujemnego jest prawie takie samo jak eksperyment dwumianowy z jedną różnicą: eksperyment dwumianowy ma stałą liczbę prób.

Jeśli pięć następujących warunków jest prawdziwych, eksperyment jest dwumianowy:

1. Stała liczba n prób.
2. Każda próba jest niezależna.
3. Możliwe są tylko dwa wyniki (sukces i porażka).
4. Prawdopodobieństwo sukcesu (p) dla każdej próby jest stałe.
5. Zmienna losowa Y= liczba sukcesów.

Przykład: Weź standardową talię kart, potasuj ją i wybierz kartę. Wymień kartę i powtórz czynność dwadzieścia razy. Y to liczba asów, które wylosowałeś.

Ujemny dwumian jest podobny do dwumianu z dwiema różnicami (w szczególności do numerów 1 i 5 na powyższej liście):

• Liczba prób, n nie jest stała.
• Zmienna losowa Y= liczba prób potrzebna do osiągnięcia r sukcesów.

Przykład: Weź standardową talię kart, potasuj ją i wybierz kartę. Wymień kartę i powtarzaj to, aż wylosujesz dwa asy. Y jest liczbą prób wyciągnięcia kart potrzebnych do wylosowania dwóch asów. Ponieważ liczba prób nie jest stała (tzn. zatrzymujesz się, gdy wylosujesz drugiego asa), jest to ujemny rozkład dwumianowy.

Co to jest ujemny rozkład dwumianowy?

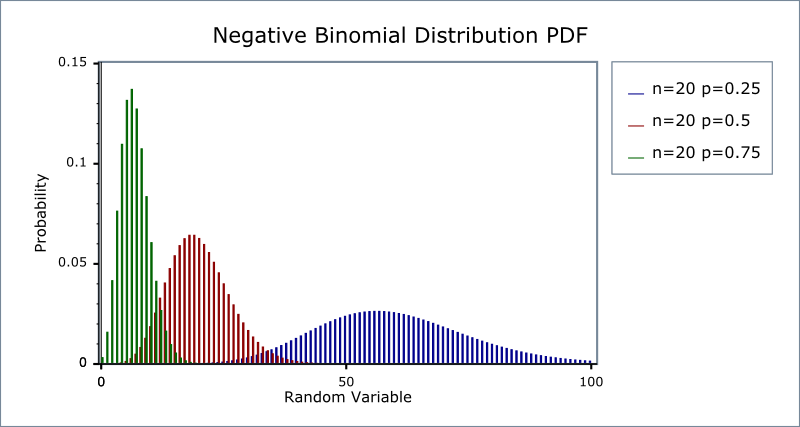
Ujemny rozkład dwumianowy (nazywany również rozkładem Pascala) jest dyskretnym rozkładem prawdopodobieństwa dla zmiennych losowych w ujemnym eksperymencie dwumianowym.

Zmienna losowa to liczba powtórzonych prób, X, które dają pewną liczbę sukcesów, r. Innymi słowy, jest to liczba porażek przed sukcesem. Jest to główna różnica w stosunku do rozkładu dwumianowego: w przypadku zwykłego rozkładu dwumianowego, patrzymy na liczbę sukcesów. W przypadku ujemnego rozkładu dwumianowego, liczy się liczba porażek.

Dlaczego nazywamy go ujemnym rozkładem dwumianowym?

Kiedy słyszysz termin ujemny, możesz pomyśleć, że rozkład dodatni jest odwrócony na osi x, co czyni go ujemnym. Jednak „negatywna” część negatywnego dwumianu wynika z faktu, że jeden aspekt rozkładu dwumianowego jest odwrócony: w eksperymencie dwumianowym liczymy liczbę sukcesów w ustalonej liczbie prób; w powyższym przykładzie liczymy, ile asów wylosowaliśmy. W eksperymencie dwumianowym ujemnym liczymy Porażki, czyli ile kart potrzeba, aby wylosować dwa asy.

Wzór na ujemny dwumian

Prawdopodobieństwo:
b*(x; r, P) = x-1Cr-1 * Pr * (1 – P)x – r
gdzie x=liczba prób
r = Sukcesy

Średnia:
μ = r / P
gdzie r jest liczbą prób
P=prawdopodobieństwo sukcesu dla dowolnej próby

Rozwiązywanie problemów z eksperymentem ujemnym dwumianowym

Pmf dla rozkładu ujemnego dwumianowego wynosi: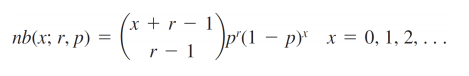

Gdzie:
r oznacza liczbę sukcesów, a
p = prawdopodobieństwo sukcesu.

Przykładowe pytanie: Badasz ludzi wychodzących z kabiny wyborczej i pytasz ich, czy głosowali niezależnie. Prawdopodobieństwo (p), że dana osoba głosowała na niezależnych wynosi 20%. Jakie jest prawdopodobieństwo, że trzeba przepytać 15 osób zanim znajdziemy 5 osób, które głosowały na niezależnych?

Krok 1: Znajdź p, r i X.
Dane jest nam (w pytaniu), że p = 20%(.2) i r = 5. Liczba niepowodzeń, X, wynosi 15 – 5 = 10.

Krok 2: Wstaw te wartości z kroku 1 do wzoru:

Krok 3: Rozwiąż. Pierwsza część (14 na 4) jest kombinacją (skorzystaj z naszego kalkulatora kombinacji, aby znaleźć 14 wybierz 4).
1001*.25*.810 = 0.034.

Prawdopodobieństwo, że będziesz musiał zapytać 15 osób, aby uzyskać 5 głosów na niezależnych wynosi .034, czyli 3.4%.

Rozkład geometryczny jest szczególnym przypadkiem ujemnego rozkładu dwumianowego.

—————————————————————————–

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania krok po kroku na swoje pytania od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!