Tetraeder

Inhaltsverzeichnis

Wir bei Cuemath glauben, dass Mathematik eine Lebenskompetenz ist. Unsere Mathe-Experten konzentrieren sich auf das „Warum“ hinter dem „Was“. Schüler können aus einem riesigen Angebot an interaktiven Arbeitsblättern, Anschauungsmaterial, Simulationen, Übungstests und mehr wählen, um ein Konzept in der Tiefe zu verstehen.

Buchen Sie noch heute eine KOSTENLOSE Probestunde und erleben Sie den LIVE-Online-Unterricht von Cuemath mit Ihrem Kind.

Ein Tetraeder ist einer der fünf platonischen Körper.

Es hat Dreiecke als Flächen.

Ein Tetraeder ist eine dreidimensionale Form, bei der alle Flächen Dreiecke sind.

Netz eines Tetraeders

Lassen Sie uns eine kleine Übung machen.

Nehmen Sie ein Blatt Papier.

Sie können zwei verschiedene Netze eines Tetraeders beobachten, die unten abgebildet sind.

Kopieren Sie dies auf das Blatt Papier.

Schneiden Sie es entlang des Randes aus und falten Sie es wie in der Abbildung unten gezeigt.

Das gefaltete Papier bildet einen Tetraeder.

Die folgende Simulation zeigt einen Tetraeder in 3D.

Klicken Sie auf den Rand des Tetraeders und ziehen Sie ihn herum.

Was sehen Sie?

Sie können alle 4 Flächen des Tetraeders sehen, während es sich dreht.

Ein normales Tetraeder hat gleichseitige Dreiecke als Flächen.

Da es aus gleichseitigen Dreiecken aufgebaut ist, messen alle Innenwinkel des Tetraeders

Ein unregelmäßiges Tetraeder hat auch dreieckige Flächen, aber sie sind nicht gleichseitig.

Die Innenwinkel des Tetraeders addieren sich in jeder Ebene, da sie dreieckig sind.

Wenn ein Tetraeder nicht ausdrücklich als unregelmäßig erwähnt wird, wird standardmäßig davon ausgegangen, dass alle Tetraeder regelmäßige Tetraeder sind.

• Es hat 4 Flächen, 6 Kanten und 4 Ecken.
• Alle vier Eckpunkte sind gleich weit voneinander entfernt.
• An jedem seiner Eckpunkte treffen sich 3 Kanten.
• Es hat 6 Symmetrieebenen.
• Im Gegensatz zu anderen platonischen Körpern hat ein Tetraeder keine parallelen Flächen.
• Ein regelmäßiges Tetraeder hat gleichseitige Dreiecke für alle seine Flächen.

Nachfolgend sind verschiedene Tetraederformeln aufgeführt.

Betrachten Sie ein regelmäßiges Tetraeder, das aus gleichseitigen Dreiecken mit der Seite s besteht.

Volumen des Tetraeders:

(\text{Volumen} = \frac{s^3}{6\sqrt{2}}\)

Gesamtoberfläche eines Tetraeders:

(\text{TSA} = \sqrt{3} \:s^2 \)

Fläche einer Fläche eines Tetraeders:

(\text{ Fläche einer Fläche } = \frac {\sqrt{3}}{4}s^2 \)

Schenkelhöhe ’s‘ eines Tetraeders:

Schräghöhe ’s‘ eines Tetraeders: \frac {\sqrt{3}}{2}s\)

Höhe ‚h‘ eines Tetraeders:

(\text{ Höhe} = \frac {s\sqrt{6}}{3}\)

Nutzen Sie den Tetraeder-Rechner, um das Volumen und die Gesamtoberfläche zu ermitteln.

Geben Sie die Kantenlänge in den Rechner unten ein.

Helfen Sie Ihrem Kind mit dem kostenlosen Diagnosetest von Cuemath zu besseren Ergebnissen. Erhalten Sie Zugang zu detaillierten Berichten, maßgeschneiderten Lernplänen und einer KOSTENLOSEN Beratungssitzung. Probieren Sie den Test jetzt aus.

Beispiel 1

Zwei kongruente Tetraeder werden entlang ihrer Grundfläche zu einer dreieckigen Bipyramide zusammengeklebt.

Wie viele Flächen, Kanten und Scheitelpunkte hat diese Bipyramide?

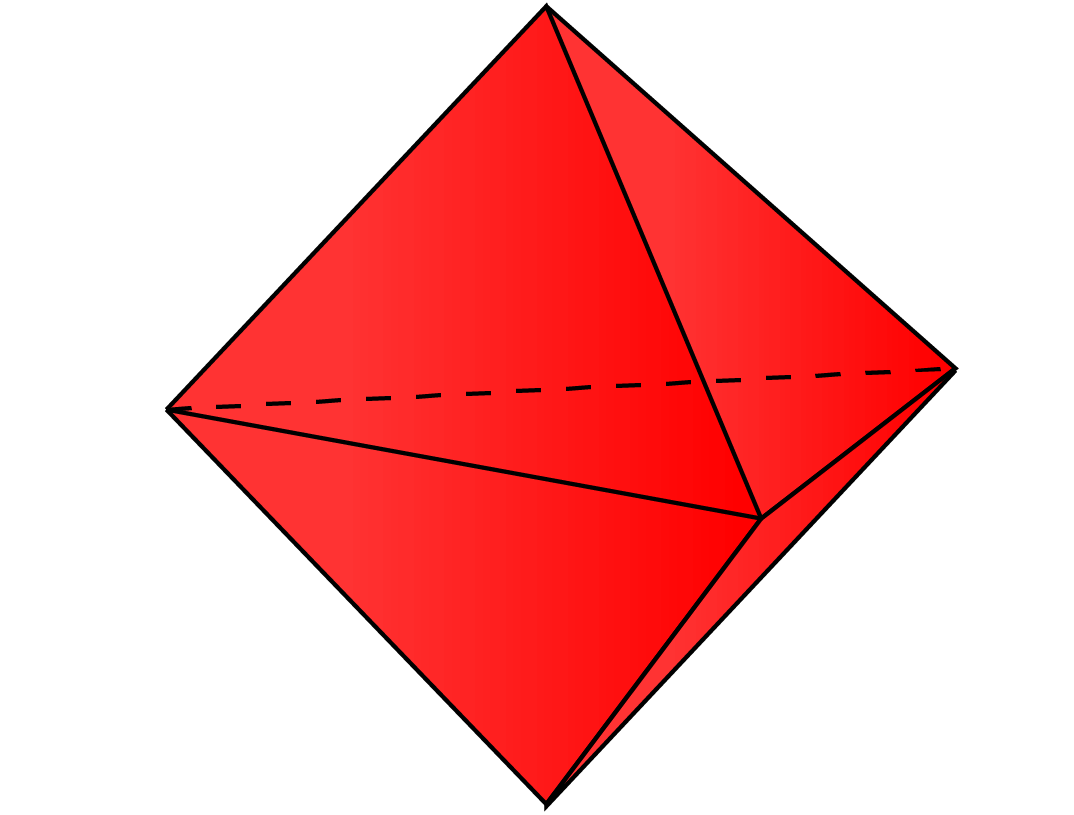
Lösung:

Wenn wir das obige Bild öffnen, um das Netz der dreieckigen Bipyramide zu sehen, können wir feststellen, dass:

Es gibt 6 dreieckige Flächen, 9 Kanten und 5 Eckpunkte.

Eine dreieckige Bipyramide hat 6 dreieckige Flächen, 9 Kanten und 5 Scheitelpunkte.

Beispiel 2

Bestimme das Volumen eines regelmäßigen Tetraeders mit einer Seitenlänge von 5 Einheiten.

(Runden Sie die Antwort auf 2 Nachkommastellen)

Lösung:

Wir wissen, dass das Volumen des Tetraeders, dessen Seite \(s\) ist:

\(\begin{align}\text{Volumen} = \frac{s^3}{6\sqrt{2}}\end{align}\)

Setzt man \(s\) als 5 ein, erhält man

\

Das Volumen des Tetraeders beträgt 14.73 Einheiten3

Beispiel 3

Jede Kante eines regelmäßigen Tetraeders hat eine Länge von 6 Einheiten.

Bestimmen Sie seinen gesamten Flächeninhalt.

Lösung:

Der Gesamtoberflächeninhalt eines regelmäßigen Tetraeders der Seite \(s\)

\(\text{TSA} = \sqrt{3}s^2 \)

Setzt man s = 6 ein, erhält man

\

Gesamtoberfläche = 62.35 Einheiten2

Beispiel 4

Die Summe der Kantenlängen eines regelmäßigen Tetraeders beträgt 60 Einheiten.

Bestimmen Sie den Flächeninhalt einer seiner Seiten.

Lösung:

Wir wissen, dass ein regelmäßiges Tetraeder 6 Kanten hat.

Daher ist die Länge jeder Kante:

\(\begin{align}\frac{60}{6} = 10 \text{ units}\end{align}\)

Oberflächeninhalt einer Fläche des Tetraeders:

\(\begin{align}\text{ Fläche einer Fläche } = \frac {\sqrt{3}}{4}s^2 \end{align}\)

Setzt man s = 10 ein, erhält man:

\

Flächeninhalt einer der Flächen = 8.66 Einheiten2

Beispiel 5

Für welches Kantenmaß ist der Gesamtflächeninhalt eines Tetraeders gleich seinem Volumen?

Lösung:

Wir wissen, dass \(\text{TSA} = \sqrt{3}s^2 \) und \(\begin{align}\text{Volumen} = \frac{s^3}{6\sqrt{2}}\end{align}\)

Wenn TSA = Volumen, können wir sagen, dass:

\( \sqrt{3} \:s^2 = \frac{s^3}{6\sqrt{2}})

Auflösen für s, haben wir

\

Kantenlänge eines Tetraeders ist \(6\sqrt6\)

Los in Mathe? Schauen Sie sich an, wie die CUEMATH-Lehrer Ihrem Kind mit interaktiven Simulationen & Arbeitsblättern das Tetraeder erklären, damit es nie wieder etwas in Mathe auswendig lernen muss!

Entdecken Sie Cuemath Live, interaktiven & personalisierten Online-Unterricht, um Ihr Kind zu einem Mathe-Experten zu machen. Buchen Sie noch heute eine KOSTENLOSE Probestunde!

Hier sind ein paar Aktivitäten zum Üben für Sie.

Wählen Sie Ihre Antwort aus und klicken Sie auf die Schaltfläche „Antwort prüfen“, um das Ergebnis zu sehen.

• IMO Musterpapier Klasse 1
• IMO Musterpapier Klasse 2
• IMO Musterpapier Klasse 3
• IMO Musterpapier Klasse 4
• IMO Musterpapier Klasse 5
• IMO Musterpapier Klasse 6
• IMO Musterpapier Klasse 7
• IMO Sample Paper Class 8
• IMO Sample Paper Class 9
• IMO Sample Paper Class 10

Um mehr über die Mathematik-Olympiade zu erfahren, können Sie hier klicken